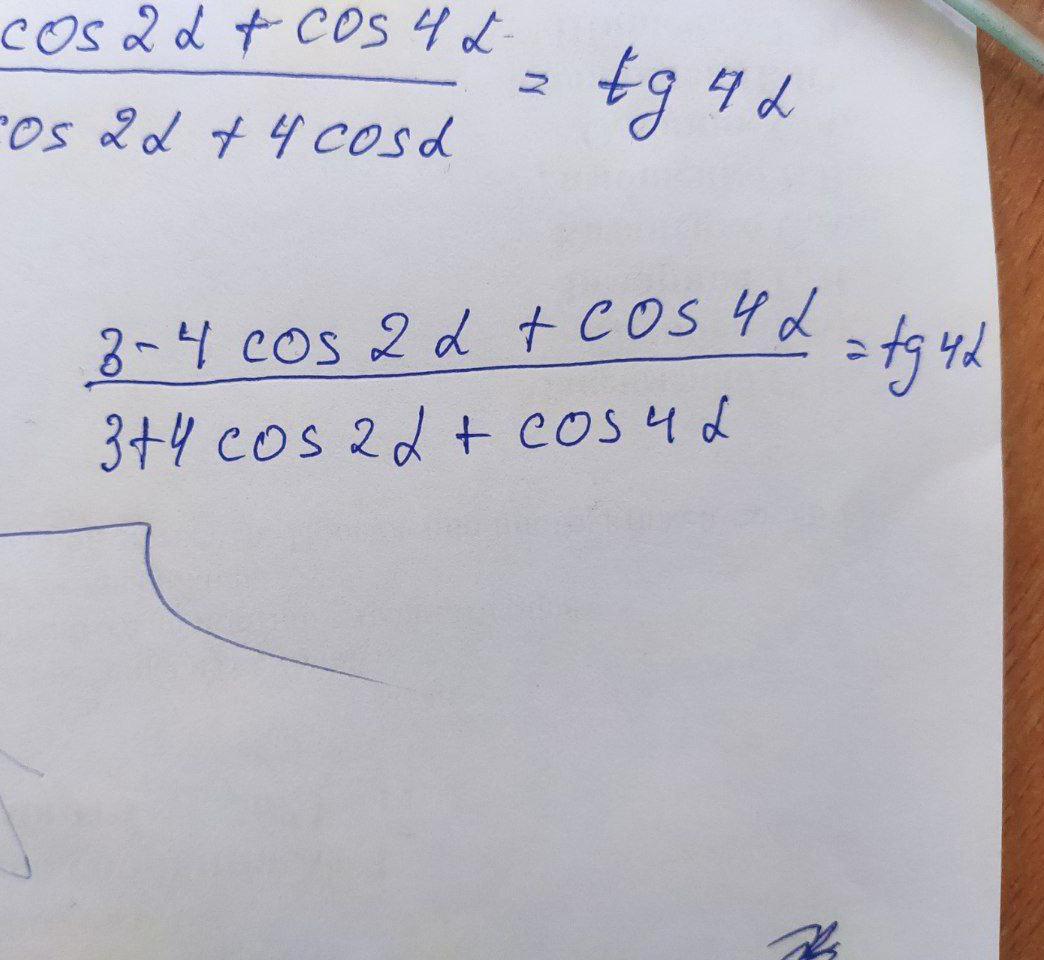Ответы
Ответ дал:
1
1) cos4a=cos2×2a=cos²2a-sin²2a=
2cos²2a-1.
2) 3-4cos2a+ 2cos²2a-1=
2cos²2a-4cos2a+→
2(cos²2a-2cos2a+1)=
2(cos2a-1)².
3) 3+4cos2a+2cos²2a-1=
2cos²2a+4cos2a+2. →
2(cos²2a+2cos2a+1)=
2(cos2a-1)².
↓
2(cos2a-1)²/2(cos2a+1)=
((cos²a-sin²a-1)/(cos²a-sin²a+1))² =
((1-sin²a-sin²a-1)/(1-sin²a-sin²a+1))²=
((-2sin²a)/(2(1+sin²a))).²=
(-sin²a/cos²a)=
tg⁴a:)))
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад