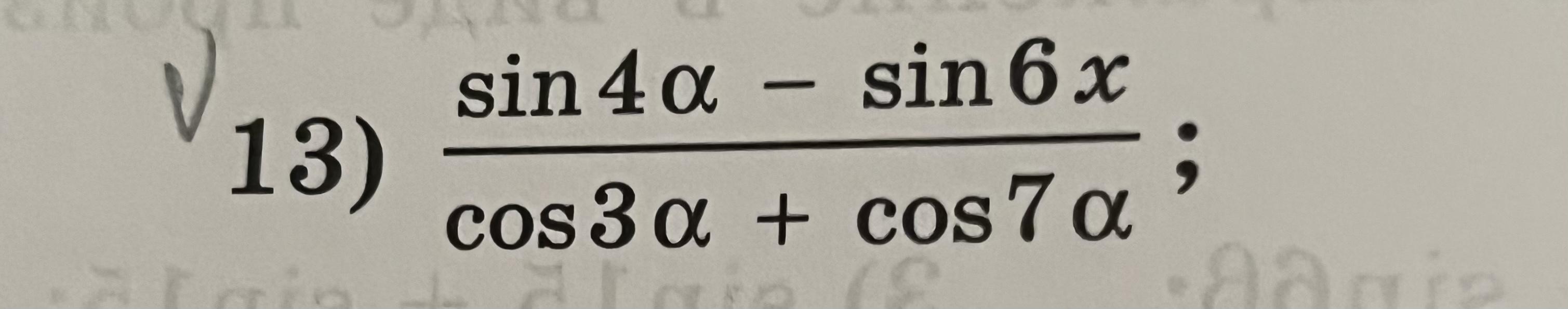Question

ПОМОГИТЕ, МОЖНО ПОЛНОЕ РЕШЕНИЕ, ОЧЕНЬ СРОЧНО.

Answer 1

Ответ:

Применим формулы разности синусов и суммы косинусов . И учтём нечётность функции синус и чётность функции косинус .

$\bf \dfrac{sin4a-sin6a}{cos3a+cos7a}=\dfrac{2\, sin\dfrac{4a-6a}{2}\cdot cos\dfrac{4a+6a}{2}}{2\, cos\dfrac{3a+7a}{2}\cdot cos\dfrac{3a-7a}{2}}=\dfrac{sin(-a)\cdot cos5a}{cos5a\cdot cos(-2a)}=\\\\\\=\dfrac{-sina}{cos2a}=-\dfrac{sina}{cos2a}$