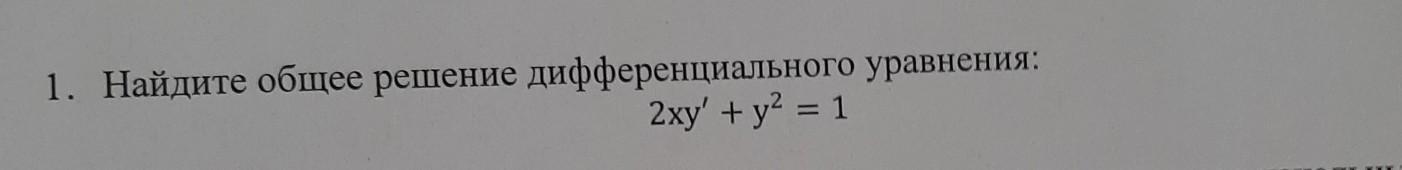Question

2ху'+у²=1
найдите общее решение дифференциального уравнения:​

Answer 1

Ответ:

Перенесем все члены с y' на одну сторону уравнения и поделим на 2x:

y' = (1-y^2)/(2x)

Обозначим u = y^2 - 1, тогда:

du/dx = 2y*y'

Подставим y' из исходного уравнения:

du/dx = -u/x

Разделим обе части на u и проинтегрируем:

du/u = -dx/x

ln|u| = -ln|x| + C

ln|y^2-1| = -ln|x| + C

y^2 - 1 = C/x^2

Таким образом, общее решение уравнения:

y = ±sqrt(1 + C/x^2)