Question

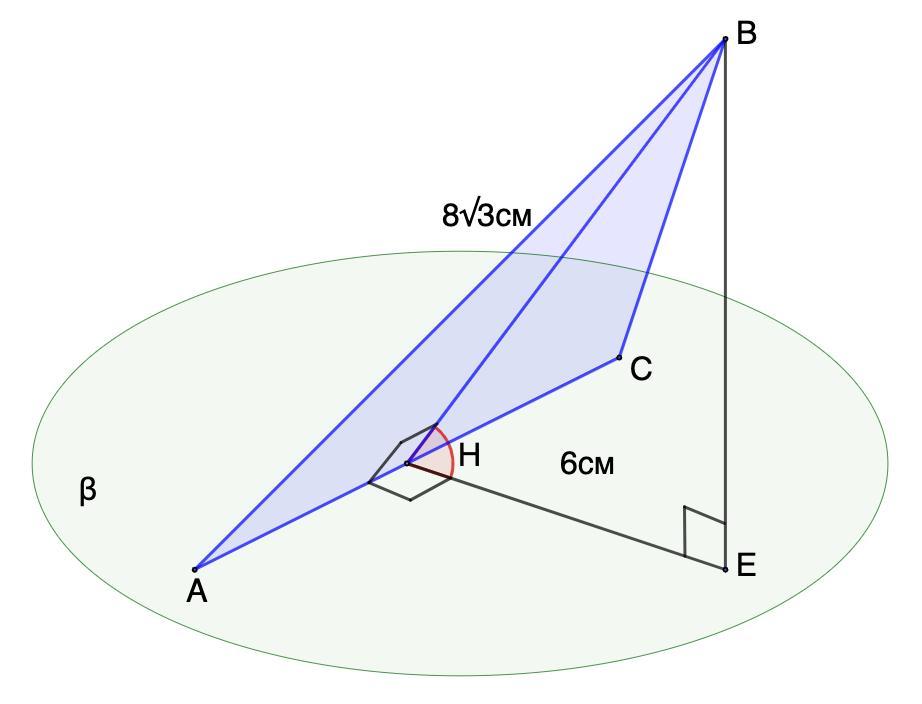
Сторона AC рівностороннього трикутника ABC лежить у площині β, а основа перпендикуляра, проведеного з точки B до площини β, віддалена від сторони AC на відстань 6 см. Обчисліть кут між площиною трикутника і площиною β, якщо AB = 8√3 см..

Answer 1

Ответ:

Угол между плоскостью треугольника и плоскостью β равен 60°.

Объяснение:

Сторона AC равностороннего треугольника ABC лежит в плоскости β, а основание перпендикуляра, проведенного от точки B к плоскости β, удалено от стороны AC на расстояние 6 см. Вычислите угол между плоскостью треугольника и плоскостью β, если AB = 8√3 см.

Дано: ΔАВС - равносторонний;

АС ∈ β; ВЕ ⊥ β;

ЕН = 6 см; АВ = 8√3 см.

Найти: угол между (АВС) и β.

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ ЕН ⊥ АС.

Соединим Н и В.

• Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.

⇒ ВН ⊥ АС.

• Угол между плоскостями — это угол между перпендикулярами,  которые лежат в данных плоскостях, проведенными к линии пересечения плоскостей,

⇒ искомый ∠ВНЕ.

Рассмотрим ΔАВС - равносторонний.

ВН - высота.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ АН = НС = 4√3 см.

Рассмотрим ΔАВН - прямоугольный.

По теореме Пифагора найдем ВН:

ВН² = АВ² - АН² = 64 · 3 - 16 · 3 = 144   ⇒   ВН = 12 см.

Рассмотрим ΔНВЕ - прямоугольный.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\angle BHE = \frac{HE}{HB}=\frac{6}{12}=\frac{1}{2}\\ \\ \angle BHE=arccos\frac{1}{2} =60^0$

Угол между плоскостью треугольника и плоскостью β равен 60°.