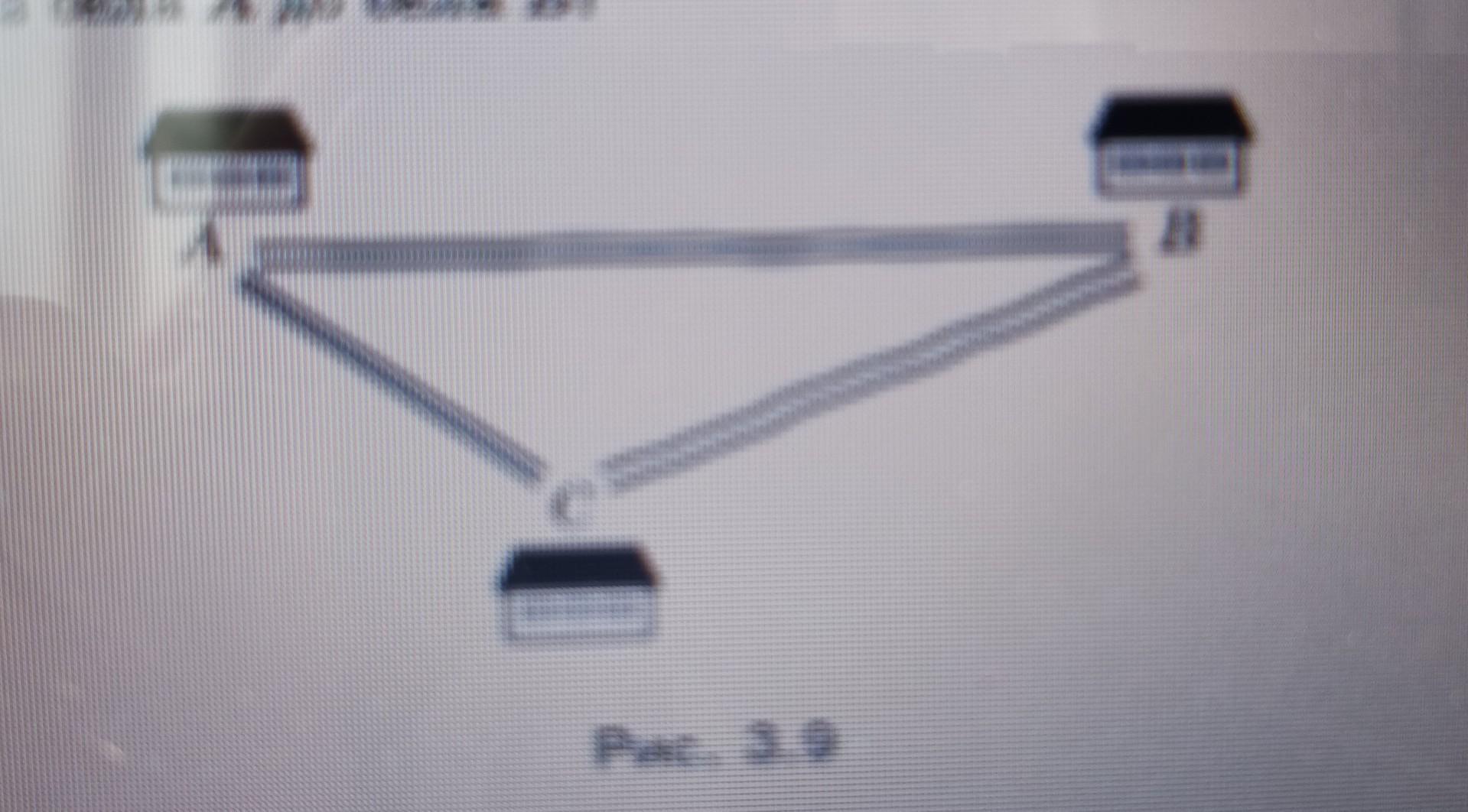
3.33." Дороги, які сполучають села А, В і С (рис. 3.9), утворюють трикутник, причому дорога iз села A до села C залофальтован а дороги із села A до села В та із села в с грунтові. Дороги, які ведуть із села A до сіл В і С. утворюють кут, величи на якого 15°, а дороги, які ведуть із села B до сіл A і C. кут. величина якого 5°. Швидкість руху автомобіля по пофальтов дором у 2 рази більша за швидкість його руху по грунтовій. Який шлях вибрати водію автомобіля, щоб яккайшанд д татися із села A до села B
Приложения:
Ответы
Ответ дал:
2
Позначимо сторони трикутника ABC як AB, AC і BC, а їх довжини як a, b і c відповідно. За теоремою косинусів для трикутника ABC:
cos A = (b^2 + c^2 - a^2) / 2bc
cos B = (a^2 + c^2 - b^2) / 2ac
cos C = (a^2 + b^2 - c^2) / 2ab
Для кута A маємо:
cos A = cos 15° = 0,966
Для кута B маємо:
cos B = cos 5° = 0,996
За теоремою синусів для трикутника ABC:
a / sin A = b / sin B = c / sin C
Тому:
b = a * sin B / sin A
c = a * sin C / sin A
Швидкість руху по залофальтованій дорозі є в два рази більшою, ніж по грунтовій, тому час, необхідний для проїзду дороги AC, буде на 50% меншим, ніж час, необхідний для проїзду доріг AB або BC.
Для обчислення часу, необхідного для проїзду кожної дороги, скористаємося формулою:
час = відстань / швидкість
Тоді час проїзду дороги AC буде:
t_AC = c / (2v)
Для дороги AB маємо:
t_AB = a / v
Для дороги BC маємо:
t_BC = b / v
Таким чином, щоб найшвидше дістатися від села A до села B, потрібно вибрати дорогу з найменшим часом проїзду. Це можна зробити, обчисливши час проїзду кожної з доріг і порівнявши їх.
Оскільки дорога AC залофальтована, її час проїзду буде на 50% меншим, ніж час проїзду доріг
cos A = (b^2 + c^2 - a^2) / 2bc
cos B = (a^2 + c^2 - b^2) / 2ac
cos C = (a^2 + b^2 - c^2) / 2ab
Для кута A маємо:
cos A = cos 15° = 0,966
Для кута B маємо:
cos B = cos 5° = 0,996
За теоремою синусів для трикутника ABC:
a / sin A = b / sin B = c / sin C
Тому:
b = a * sin B / sin A
c = a * sin C / sin A
Швидкість руху по залофальтованій дорозі є в два рази більшою, ніж по грунтовій, тому час, необхідний для проїзду дороги AC, буде на 50% меншим, ніж час, необхідний для проїзду доріг AB або BC.
Для обчислення часу, необхідного для проїзду кожної дороги, скористаємося формулою:
час = відстань / швидкість
Тоді час проїзду дороги AC буде:
t_AC = c / (2v)
Для дороги AB маємо:
t_AB = a / v
Для дороги BC маємо:
t_BC = b / v
Таким чином, щоб найшвидше дістатися від села A до села B, потрібно вибрати дорогу з найменшим часом проїзду. Це можна зробити, обчисливши час проїзду кожної з доріг і порівнявши їх.
Оскільки дорога AC залофальтована, її час проїзду буде на 50% меншим, ніж час проїзду доріг
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад