Question

Даю 100 баллов за решение, 2 задачи по геометрии

Answer 1

Ответ:

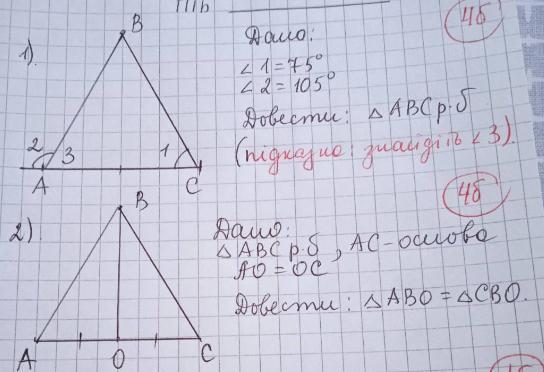
1)  ΔАВС ,  ∠1 = ∠АСВ = 75°  ,  ∠2 = 105° , ∠2 - внешний угол ΔАВС , смежный с ∠ВАС = ∠3 .  Доказать, что ΔАВС - равнобедренный .

 Вычислим ∠3 . Воспользуемся тем, что сумма смежных углов равна 180° .

∠2 + ∠3 = 180°    ⇒    ∠3 = 180°- ∠2 = 180° - 105° = 75°  

Получили , что в  ΔАВС  есть два равных угла при стороне АС .

Значит,   ΔАВС  равнобедренный  и АВ = ВС  .

2)   ΔАВС - равнобедренный , АС - основание  ⇒   АВ = ВС  ,

АО = ОС .  Доказать, что  ΔАВО = ΔСВО  .

Так как  ΔАВС равнобедренный  и АВ = ВС , то  углы при основании равны, то есть  ∠ВАС = ∠ВСА .

Имеем :  АВ = ВС  ,  АО = ОС  ,  ∠ВАС = ∠ВСА  .

Отсюда следует, что ΔАВО = ΔСВО по 1 признаку равенства треугольников , по двум сторонам и углу между ними .      

Answer 2

1.

∠3=180-∠2=180-105=75° за  властивістю суміжних кутів

∠1=∠2=75°, отже ΔАВС - рівнобедрений. Кути при основі рівнобедреного трикутника рівні.

2.

ΔАВО=ΔСВО за третьою ознакою рівності трикутників (АВ=ВС за умовою, АО=СО за умовою, ВО - спільна сторона).