Знайти загальний розв’язок диференціального рівняння. (Заміна: y=zx, y’=dy/dx , dy=zdx+xdz).
Приложения:
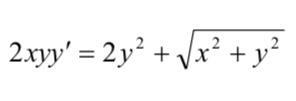
Ответы
Ответ дал:
0
Ответ:
Общий интеграл дифференциального уравнения:
Пошаговое объяснение:
------------------------------------------------------------------------------------------------------
Замена:
- не является решением дифференциального уравнения
------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
- не является решением дифференциального уравнения
------------------------------------------------------------------------------------------------------
- общий интеграл дифференциального уравнения
Вас заинтересует
1 год назад
3 года назад
3 года назад