Question

В паралелограмі з вершини гострого кута, що дорівнює 30°, проведена бісектриса, яка розділяє сторону на відрізки 12 см і 5 см, рахуючи від вершини тупого кута. Знайдіть площу паралелограма.
Помогите, пожалуйста ​

Answer 1

Ответ:

Объяснение:

Дано:

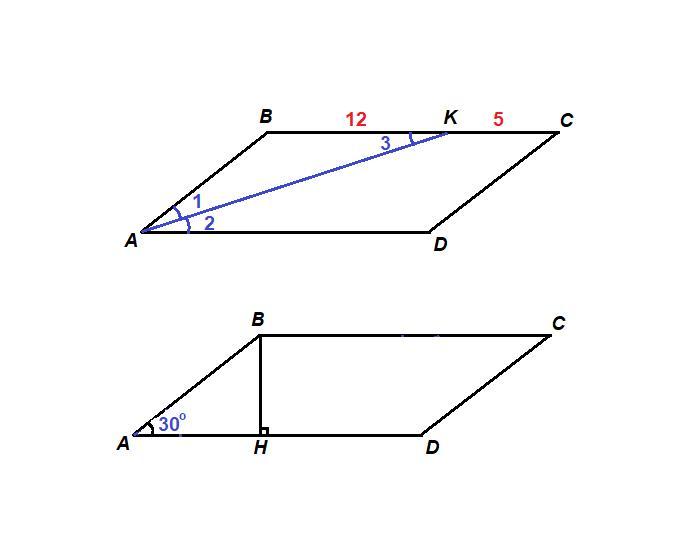
ABCD - параллелограмм,

∠BAD = 30°

AK - биссектриса, К∈ВС,

ВК = 12 см, КС = 5 см.

Найти:

$S_{ABCD}$

Решение:

• В параллелограмме противолежащие углы равны и противолежащие стороны равны.

AD = BC = BK + KC = 12 + 5 = 17 см

∠2 = ∠1, так как АК биссектриса,

∠2 = ∠3 как внутренние накрест лежащие при пересечении ВС║AD секущей АК, значит ∠1 = ∠3.

Тогда ΔАВК равнобедренный с основанием АК.

АВ = ВК = 12 см.

• Площадь параллелограмма можно найти как произведение двух сторон на синус угла между ними.

$S_{ABCD}=AB\cdot BC\cdot \sin\angle A=12\cdot 17\cdot \dfrac{1}{2}=102$

Sabcd = 102 см²

Если синусы еще не проходили, то можно и иначе:

• Площадь параллелограмма можно найти как произведение стороны на проведенную к ней высоту.

Проведем ВН - высоту параллелограмма.

ΔАВН:  ∠АНВ = 90°, ∠ВАН = 30°, тогда

ВН = 0,5 АВ = 0,5 · 12 = 6 см по свойству катета, лежащего против угла в 30°.

$S_{ABCD}=AD\cdot BH=17\cdot 6=102$

Sabcd = 102 см²