Question

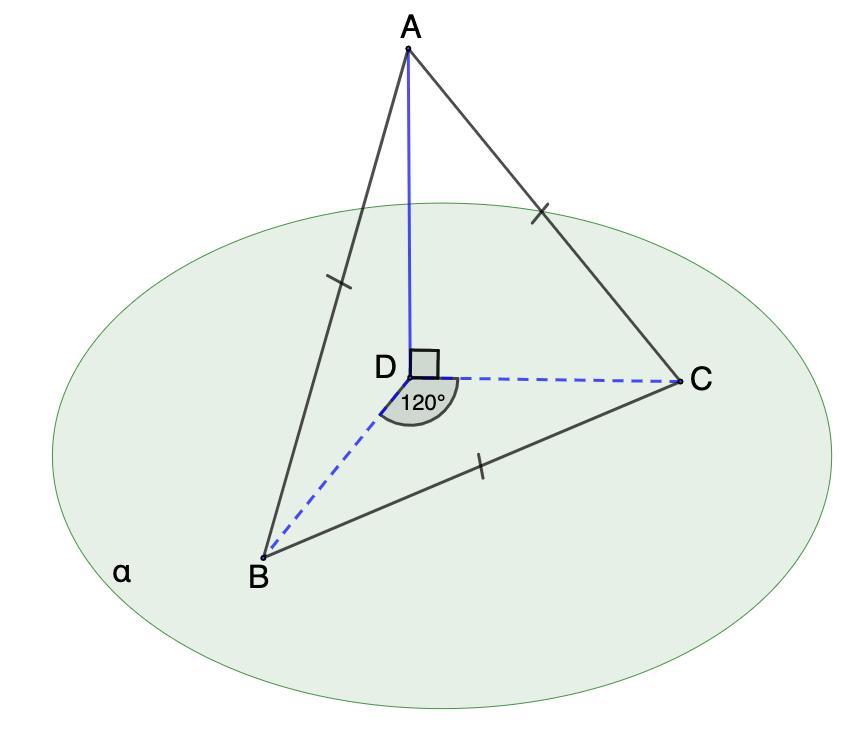
2. AB и AC
наклонные, AD перпендикулярна a,
Угол BDC = 120°, треугольник АВС -
равносторонний площади 12 корней из 3.
Найдите площадь треугольника
BDC

Answer 1

Ответ:

Площадь треугольника BDC равна 4√3 ед.².

Объяснение:

2. AB и AC - наклонные, AD перпендикулярна α. Угол BDC = 120°, треугольник АВС - равносторонний площадью 12√3.

Найдите площадь треугольника BDC.

Дано: AB и AC - наклонные;

AD ⊥ α; ΔАВС - равносторонний;

S(АBC) = 12√3.

Найти: S(BDC)

Решение:

• Площадь равностороннего треугольника равна:

                          $\displaystyle\bf S=\frac{a^2\sqrt{3} }{4}$ ,

где а - сторона треугольника.

$\displaystyle S(ABC)=\frac{BC^2\cdot \sqrt{3} }{4} \\ \\12\sqrt{3} =\frac{BC^2\cdot \sqrt{3} }{4} \\ \\ BC^2=48\\\\BC=4\sqrt{3}$

Рассмотрим ΔBDC.

• Равные наклонный, проведенные из одной точки, имеют равные проекции.

АВ = АС   ⇒   DB = DC

Пусть  DB = DC = х

• Теорема косинусов:
• Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

ВС² = DB² + DC² - 2 · DB · DC · cos ∠BDC

48 = x² + x² - 2 ·x · x · (-0,5)

48 = 3x²

x = 4

⇒  DB = DC = 4

• Площадь треугольника найдем по формуле:

                        $\displaystyle\bf S=\frac{1}{2} ab\;sin\alpha$ ,

где а и b - стороны треугольника, α - угол между этими сторонами.

$\displaystyle S(BDC) = \frac{1}{2} \cdot4 \cdot 4\cdot sin120^0 = 8\cdot\frac{\sqrt{3} }{2}=4\sqrt{3}$   (ед.²)

Площадь треугольника BDC равна 4√3 ед.².

#SPJ1