В правильной усечённой пирамиде стороны верхнего и нижнего оснований соответственно равны 2 под корнем 3 дм и 4 под корнем 3 дм, а двугранный угол при ребре нижнего основания равен 60 градусов. Найдите объём пирамиды,если она: а)четырёхугольная;б) треугольная (спасибо за решение)

Ответы
V =1/3 Sо H
Усеченную пирамиду рассмотрим как разность большой и малой пирамид.
Они подобны с коэффициентом 1/2 (отношение соответствующих сторон)
Объемы относятся как куб коэф подобия, 1/8
Разность объемов =7/8 объема большой пирамиды
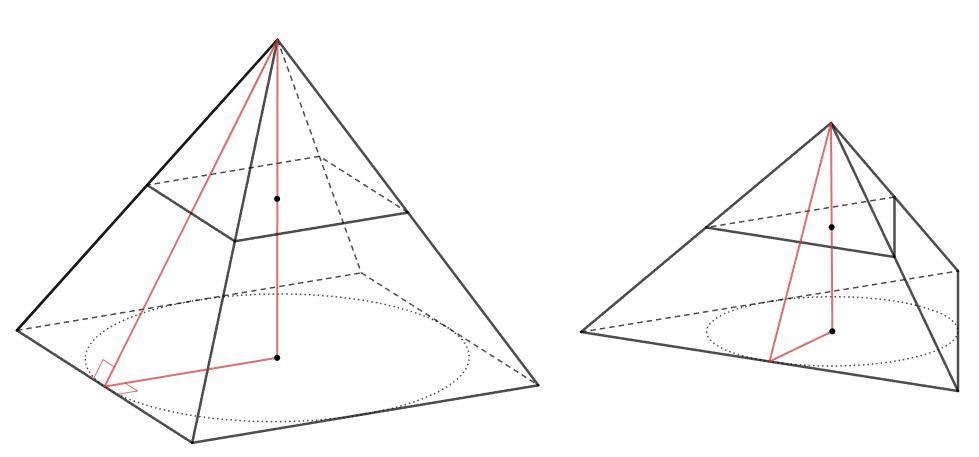
Правильная пирамида
- в основании правильный многоугольник
- вершина падает в центр основания
По теореме о трех перпендикулярах апофема, высота и радиус вписанной окружности основания образуют треугольник.
Угол между радиусом и апофемой - угол между перпендикулярами к ребру - линейный угол двугранного угла при основании, 60.
H/r =tg60 => H =√3 r
четырёхугольная, в основании квадрат
Sо =a^2
r =a/2
V усеч =7/8 ·1/3 ·a^2 ·√3 ·a/2 =7/16√3 (4√3)^3 =84 (дм^3)
треугольная, в основании равносторонний треугольник
So =√3/4 a^2
r =a/2√3
V усеч =7/8 ·1/3 ·√3/4 ·a^2 ·√3 ·a/2√3 =7/64√3 (4√3)^3 =21 (дм^3)