15. Изобразите фигуру, координаты (x; у) точек которой удовлетворяют неравенству 0 < x² + y² - 2x < 3. 30
Ответы
Ответ дал:
1
Ответ:
Неравенство можно заменить системой неравенств
Выделим полный квадрат из выражения
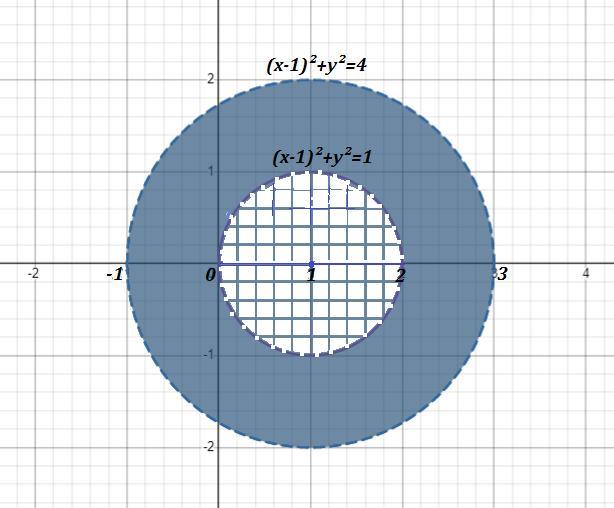
- это окружность с центром в точке (1;0) и радиусом R=1 .
- это окружность с центром в точке (1;0) и радиусом R=2 .
Значит заданная область - это кольцо между окружностями с центром в точке (1;0) и радиусами R₁=1 и R₂=2 . Причём сами окружности в область не входят, так как знак неравенства строгий. И поэтому окружности рисуем пунктирными линиями .
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад