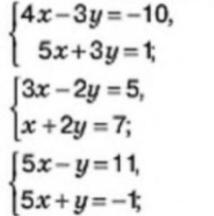Question

Помогите, дам корону
Вирішіть 3 лінійних системи за допомогою додавання

Answer 1

Для розв'язання лінійної системи за допомогою додавання необхідно складати рівняння таким чином, щоб зі змінних зникала одна з них. Для цього ми можемо помножити одне рівняння на певний коефіцієнт так, щоб його змінна збігалася за знаком зі змінною в іншому рівнянні.

У даній системі ми можемо помножити перше рівняння на 3, щоб отримати:

1)

12x - 9y = -30

Далі додаємо його до другого рівняння:

(12x - 9y) + (5x + 3y) = -30 + 1

Отримуємо:

17x = -29

Ділимо обидві частини на 17:

x = -29/17

Підставляємо значення x у будь-яке з початкових рівнянь і знаходимо y:

4x - 3y = -10

4(-29/17) - 3y = -10

-116/17 - 3y = -10

-3y = -10 * 17/17 + 116/17

-3y = -34/17

y = 34/51

Отже, розв'язок системи дорівнює:

x = -29/17

y = 34/51

2)

(3x - 2y) + (x + 2y) = 5 + 7

4x = 12

x = 3

Тепер, підставивши це значення x в будь-яке з рівнянь, можна знайти значення y. Наприклад, підставимо x = 3 в друге рівняння:

3 + 2y = 7

2y = 4

y = 2

Отже, розв'язок системи дорівнює:

x = 3

y = 2

3)

(5x - y) + (5x + y) = 11 - 5

10x = 6

x = 6/10 = 3/5

Тепер, підставивши це значення x в будь-яке з рівнянь, можна знайти значення y. Наприклад, підставимо x = 3/5 в перше рівняння:

5(3/5) - y = 11

3 - y = 11

y = -8

Отже, розв'язок системи дорівнює:

x = 3/5

y = -8