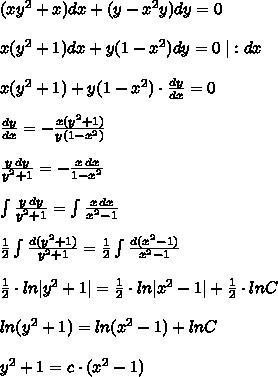Ответы
Ответ:
Дано дифференциальное уравнение первого порядка:
(xy^2 + x)dx + (y - x^2y)dy = 0
Мы можем решить его, используя метод интегрирующего множителя. Для этого нужно найти функцию μ(x,y), которая удовлетворяет уравнению:
∂(μ(xy^2 + x))/∂y = ∂(μ(y - x^2y))/∂x
То есть:
y^2μ(x) = -x^2μ'(y)
Заметим, что левая часть зависит только от y, а правая - только от x. Значит, обе части должны быть равны константе. Пусть эта константа равна -k^2, где k - произвольное число. Тогда:
y^2μ(x) = k^2
-x^2μ'(y) = -k^2
Решим второе уравнение относительно μ(y):
μ(y) = k^2/(x^2)
Теперь найдем производную μ(x):
μ'(x) = -2ky^2/x^3
Подставим μ(x) и μ'(x) в уравнение с исходной функцией и умножим его на μ(x):
k^2(dx/x^2) - 2ky^2(dy/y^2) = 0
Проинтегрируем это уравнение:
k^2ln|x| + 2k/y = C
где C - произвольная постоянная интегрирования. Разрешим ее относительно k:
k = (C - 2y/ln|x|)/ln|x|
Таким образом, общее решение уравнения имеет вид:
ln|x|^2/y + 2/ln|x| = C
где C - произвольная постоянная. Используя начальное условие y(2) = 0, получим:
ln|2|^2/0 + 2/ln|2| = C
C = -4ln(2)
Таким образом, частное решение уравнения имеет вид:
ln|x|^2/y + 2/ln|x| = -4ln(2)
Чтобы найти явную формулу для y(x), можно переписать это уравнение следующим образом:
y = x^2/(e^(2/ln|x|+4ln(2)))
или, эквивалентно,
y = x^2/(4x^2 + 1)
Таким образом, решение исходного дифференциального уравнения с начальным условием y(2) = 0 имеет вид:
y(x) = x^2/(4x^2 + 1)
Ответ:
Пошаговое объяснение:
вроде так