Помогите пожалуйста с двумя заданиями по алгебре,пожалуйста решение расписать.Заранее огромнейшее спасибо.
Приложения:
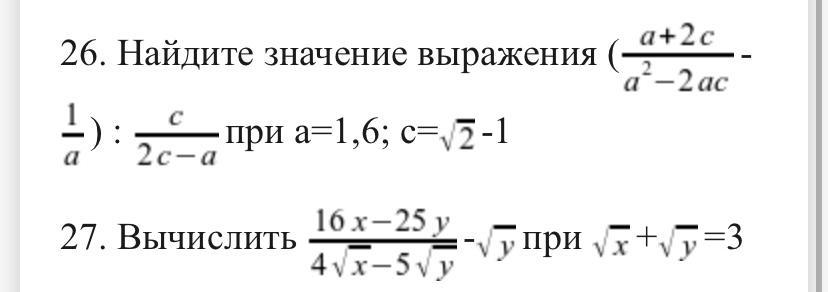
Ответы
Ответ дал:
2
Ответ:
26) Сначала упростим выражение, а потом вычислим его значение
при .
27) Вычислить значение выражения при .
Разложим числитель на множители , применив формулу разности
квадратов, учитывая, что .
gornolyznyjandrej:
спасибо большое
пожалуйста
Вас заинтересует
1 год назад
3 года назад
3 года назад
8 лет назад