45 балов ☀️☀️☀️☀️☀️☀️☀️буду благодарна! задачу решите полностью.
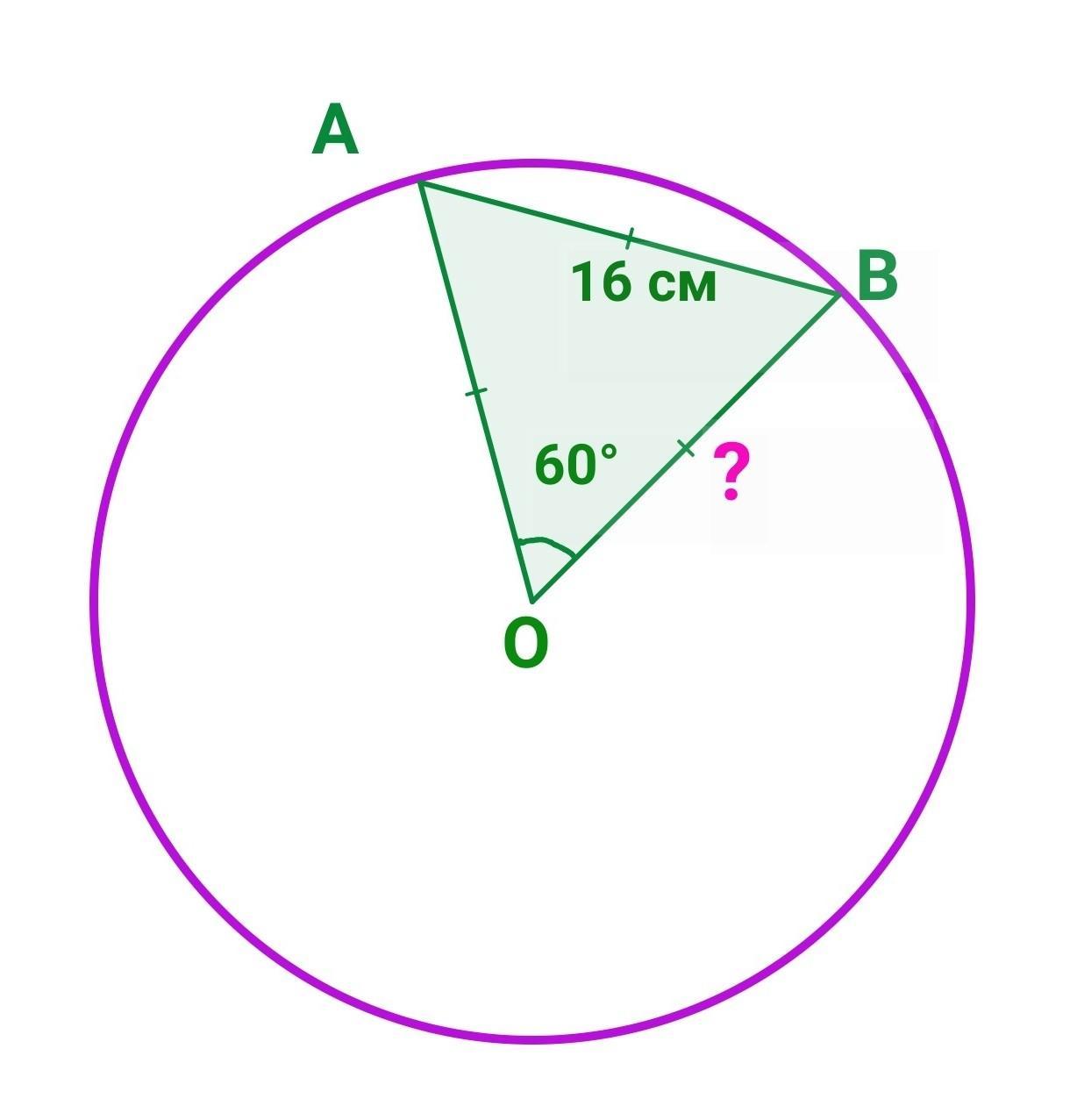
1. дано коло з центром О і хорда, яка дорівнює 16 см. кут АОВ=60°
знайти радіус цього кола і периметр трикутника АОВ.
Приложения:

Ответы
Ответ дал:
1
Ответ:
Радіус кола дорівнює 16 см
Періметр трикутника АОВ дорівнює 48 см
Объяснение:
Дано коло з центром О і хорда АВ, яка дорівнює 16 см. ∠АОВ=60°. Знайти радіус цього кола і периметр трикутника АОВ.
1.
В △АОВ АО=ОВ - як радіуси кола, отже △АОВ - рівнобедрений з основою АВ.
∠А=∠В - як кути при основі рівнобедреного трикутника.
За теоремою про суму кутів трикутника:
∠А=∠В=(180°-∠О):2=(180°-60°):2=60°
Всі кути △АОВ рівні. Отже △АОВ - рівносторонній.
АО=ОВ=АВ=16(см).
Радіус кола дорівнює 16 см.
2.
Периметр трикутника дорівнює сумі всіх його сторін:
Р(АОВ)=АО+ОВ+АВ=16+16+16=48(см)
Відповідь: 16 см; 48 см
Приложения:
vasiliva1509:
Благодарю! ☀️
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад