Ответы
Ответ дал:
2
Ответ: 180°
Решение: Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны
Окружность можно вписать только в один прямоугольник: КВАДРАТ!
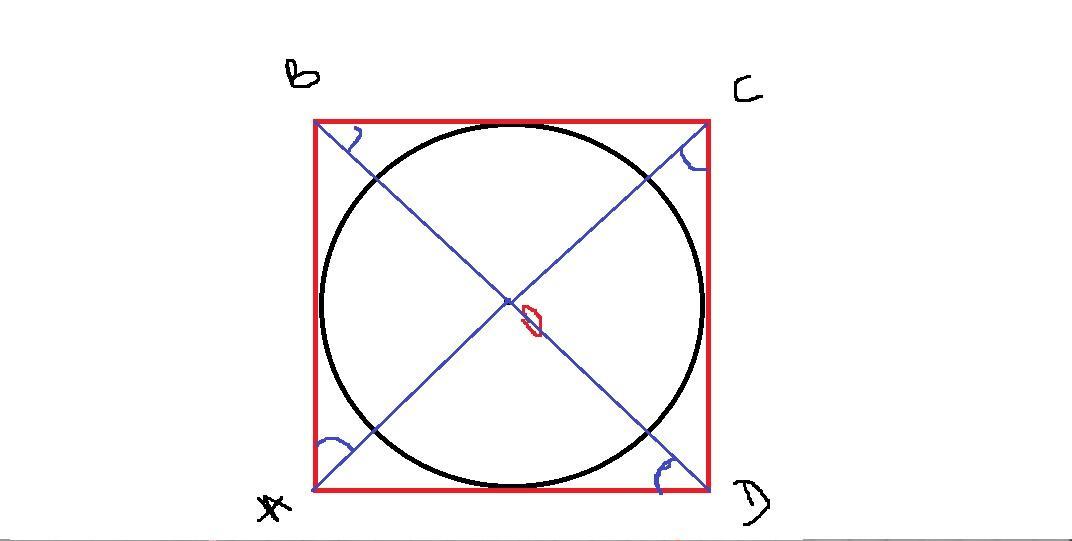
Дано: ABCD- прямоугольник, О- центр вписанной окружности
Найти: ∠OAB +∠OBC +∠OCD +∠ODA
Решение: АВСD- квадрат согласно свойству вписанной окружности( сумма противоположных сторон- равны)
ОА и ОС ∈ одной прямой- АС-диагонали квадрата, ОВ и ОВ ∈ одной прямой ВD-диагонали квадрата.
По свойству диагоналей квадрата (делят углы квадрата пополам )
∠АОВ=1/2∠А=1/2*90°=45°
∠OBC=1/2∠В=45°
∠OCD=1/2∠С =45°
∠ODA=1/2D=45°
∠OAB +∠OBC +∠OCD +∠ODA=4*45°=180°
Приложения:
top4iktopor4ik:
От души спасибо
ty
Вас заинтересует
1 год назад
3 года назад