Ответы
Ответ:
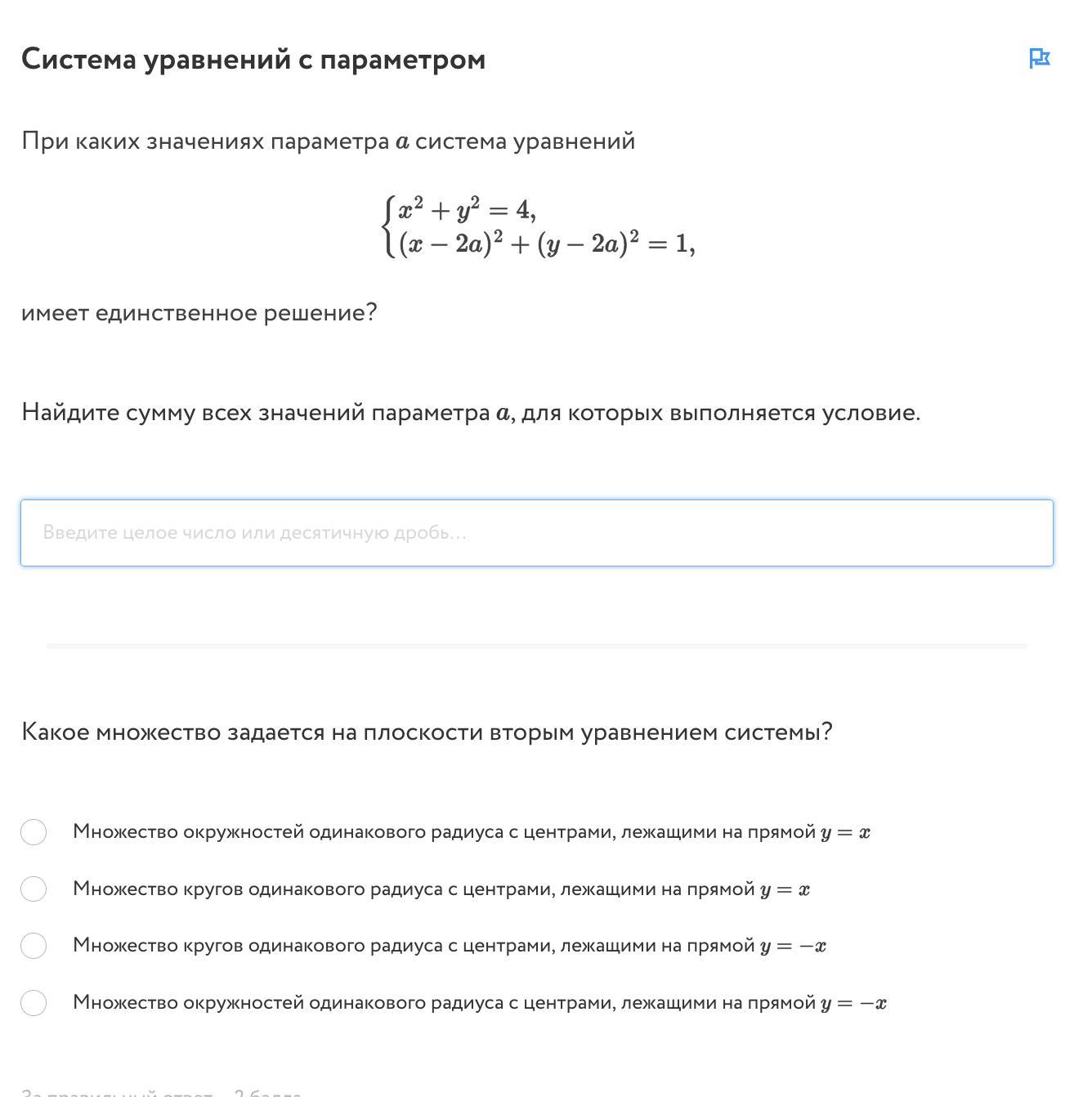
0; множество окружностей с одинаковыми радиусами, центр которых лежит на прямой y=x
Объяснение:
Первое уравнение задаёт окружность с центром (0;0) и радиусом 2
Второе задаёт окружность с центром (2a;2a) и радиусом один
пусть y0 и x0 точки центра второй окружности:
y0=2a
x0=2a => y0=x0
Это означает, что в зависимости от параметра, центр окружности будет двигаться по прямой y=x
Итак, когда же система имеет одно решение. Система имеет одно решение тогда, когда эти окружности касаются(внешним или внутренним образом), причём касание может происходить как в четверти положительных, так и в четверти отрицательных "x" и "y"
Из геометрических соображений получаем симметричные точки
Сумма всех возможных значений параметра, при которых выполняется условие, равно нулю