Question

коло вписане в рівнобедрений трикутник ділить його бічну сторону у відношенні 2:3 починаючи від вершини що протилежна основі знайдіть стороони трикутника якщо його периметр дорівнює 240

Answer 1

Ответ:

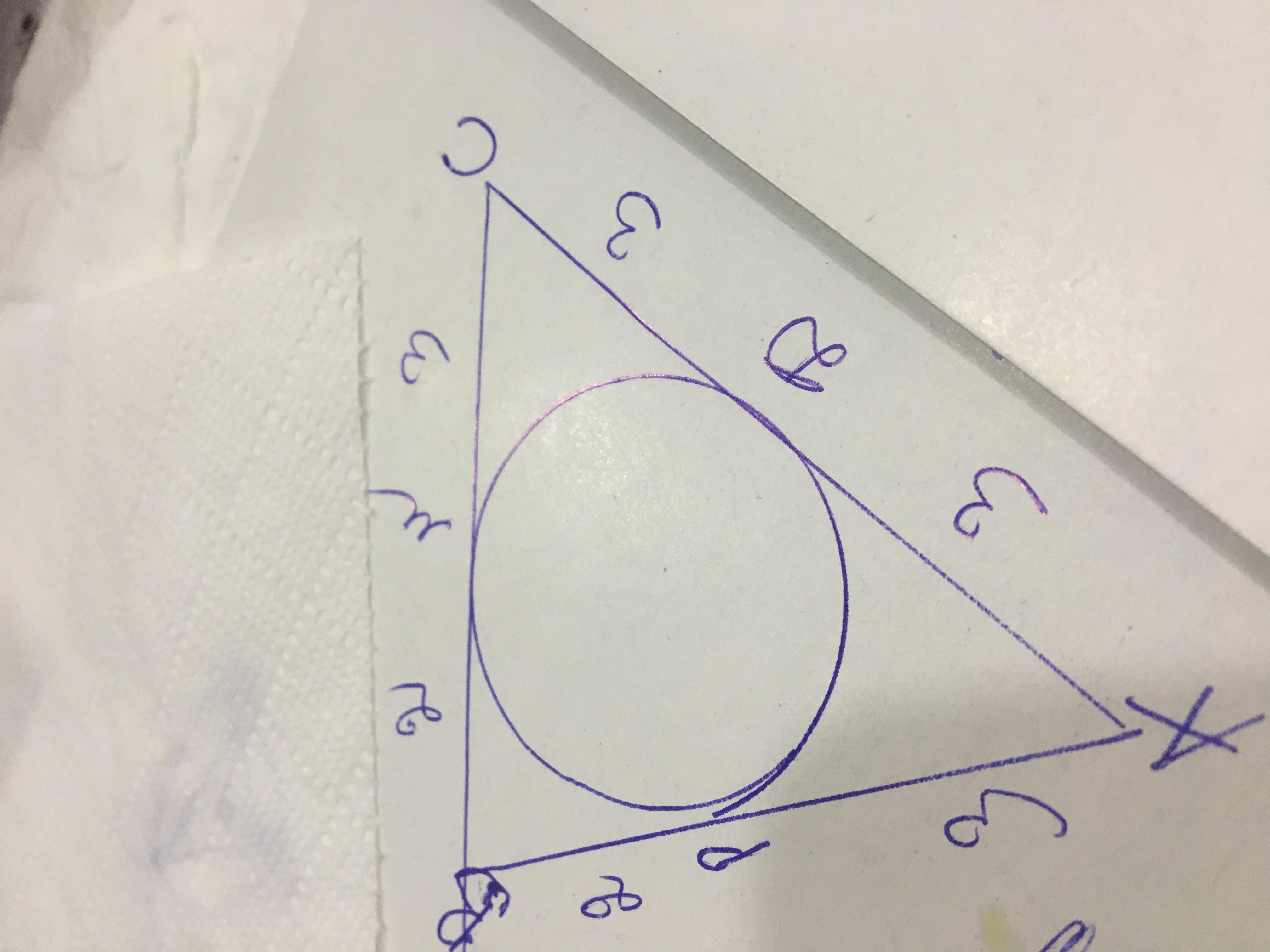
Согласно свойства касательных-если к окружности из одной точки проведены две касательные,то они равны

РВ=ВС=2

АР=АD=3

MC=DC=3

2X•2+6X•2=240

16X=240

X=240:16

X=15

AB=BC=(2+3)•15=75 ,как боковые стороны равнобедренного треугольника

Основание

АС=3•2•15=90

Р=75•2+90=240

Объяснение: