Question

Найдите велечину центрального угла,если он на 69° больше острого вписанного угла, опирающего на ту жу дугу

Answer 1

Ответ:

Центральный угол равен 138°

Объяснение:

Информация: 1) Центральный угол — угол с вершиной в центре окружности.

2) Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

3) Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

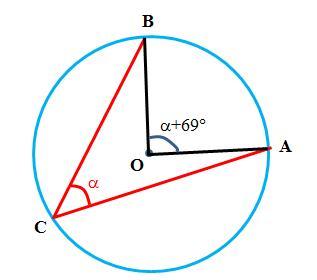
Решение. Пусть острый вписанный угол равен α. По условию центральный угол на 69° больше этого вписанного угла, то есть равен α+69° (см. рисунок).

Далее, по свойству вписанного и центрального угла опирающегося на одну и ту же дугу получим:

$\tt \alpha =\dfrac{\alpha +69^0}{2} .$

Отсюда

2·α = α + 69° или α = 69°.

Значит, центральный угол равен 69° + 69° = 138°.

#SPJ1