Використовуючи
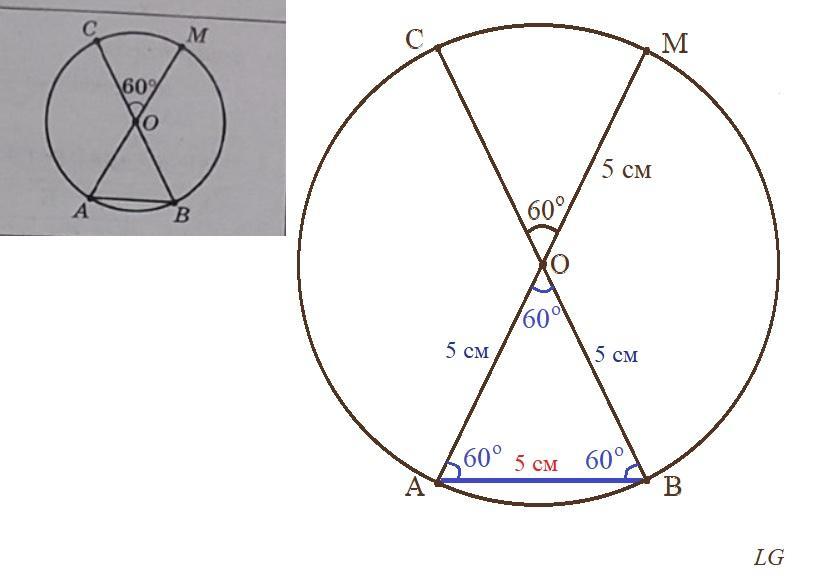
рисунок, знайдіть довжину хорди АВ, якщо кутCOM=60°,
а радіус ОМ = 5 см
Ответы
Ответ:
Хорда АВ = 5 см
Объяснение:
Перевод: Используя рисунок, найдите длину хорды АВ, если ∠COM=60°, а радиус ОМ = 5 см.
Информация: 1) Вертикальные - два угла, которые образуются при пересечении двух прямых. Два вертикальных угла равны.
2) Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.
Решение. Из рисунка видно, что OA и OB также радиусы и поэтому
OA = OB = ОМ = 5 см.
Далее, ∠AOB=∠COM=60° как вертикальные углы. Теперь применим теорему косинусов для хорды АВ:
АВ² = OA² + OB² - 2·OA·OB·cos∠AOB.
Подставим известные значения:
АВ² = 5² + 5² - 2·5·5·cos60° = 25 + 25 - 50·0,5 = 25 + 25 - 25 = 25,
отсюда АВ = 5 см.
#SPJ1
Ответ:
Хорда AB = 5 см.
Объяснение:
Используя рисунок, найти длину хорды AB, если ∠COM = 60°, а радиус OM = 5 см.
- Два угла называются вертикальными, если стороны одного из них являются дополнительными полупрямыми сторон другого угла.
- Вертикальные углы равны.
- Треугольник, у которого две стороны равны, называется равнобедренным.
- В равнобедренном треугольнике углы при основании равны.
- Сумма углов треугольника равна 180°.
По рисунку.
1) ∠AOB = ∠COM = 60° как вертикальные углы.
2) ΔAOB равнобедренный, так как стороны AO = OB = 5 см, это радиусы одной окружности.
Тогда углы его при основании равны, ∠A = ∠B.
3) Найдем углы ∠A и ∠B в ΔAOB:
∠A = ∠B = (180° - 60°) : 2 = 120° : 2 = 60°.
4) В ΔAOB все углы равны. Значит, это равносторонний треугольник.
Тогда сторона AB = 5 см.
Хорда AB = 5 см.
#SPJ1