Question

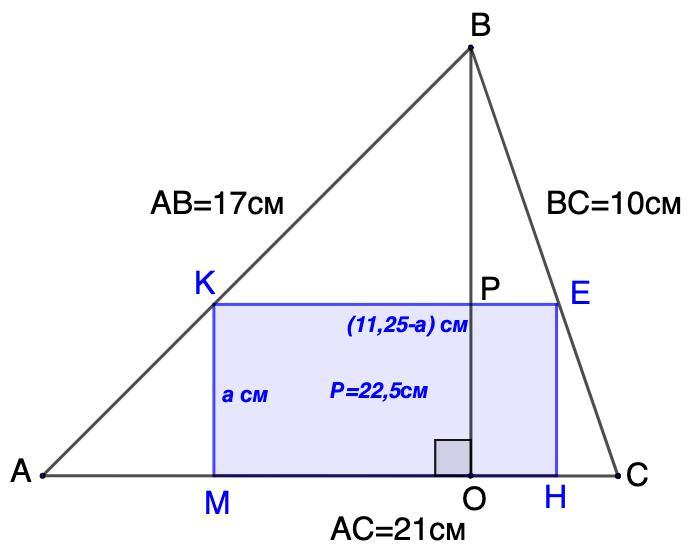
У трикутник зі сторонами 10, 17 і 21 см вписаний прямокутник так, що дві його
вершини знаходяться на одній стороні трикутника, а дві інші – на двох інших
сторонах трикутника. Знайти сторони прямокутника, якщо відомо, що його
периметр дорівнює 22,5 см.

Answer 1

Ответ:

Стороны прямоугольника равны 6см и 5,25 см.

Объяснение:

В треугольник со сторонами 10, 17 и 21 см вписан прямоугольник так, что две его вершины находятся на одной стороне треугольника, а две другие-на двух других сторонах треугольника. Найти стороны прямоугольника, если известно, что его периметр равен 22,5 см.

Дано: ΔАВС.

АВ = 17 см; ВС = 10 см; АС = 21 см;

МКЕН - прямоугольник, вписан в ΔАВС;

Р(МКЕН) = 22,5 см.

Найти: стороны прямоугольника.

Решение:

Проведем высоту ВО.

Пусть сторона МК прямоугольника МКЕН равна а см.

• Периметр прямоугольника равен удвоенной сумме смежных сторон.

                            Р = 2(а + b),

где а и b - стороны прямоугольника.

22,5 = 2(а + КЕ)      |: 2

КЕ = 11, 25 - а

Найдем площадь ΔАВС по формуле Герона:

$\displaystyle\bf S=\sqrt{p(p-a)(p-b)(p-c)} ,$

где р - полупериметр, а, b, c - стороны треугольника.

P = 10 + 17 + 21 = 48 (см)   ⇒   р = 48 : 2 = 24 (см)

$\displaystyle S=\sqrt{24(24-17)(24-10)(24-21)} =\sqrt{2\cdot4\cdot3\cdot7\cdot2\cdot7\cdot3} =\\\\=2\cdot2\cdot3\cdot7=84\;_{(CM^2)}$

С другой стороны:

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(ABC) = \frac{AC\cdot BO}{2} \\\\84=\frac{21\cdot BO}{2}\\ \\BO=\frac{168}{21} =8\;_{(CM)}$

Рассмотрим ΔАВС и ΔКВЕ.

∠В - общий;

∠ВКЕ = ∠А (соответственные при КЕ || AC и секущей АВ)

⇒ ΔКВЕ ~ ΔАВС (по двум углам)

• Отношение длин высот, биссектрис и медиан подобных треугольников равно коэффициенту подобия k.

$\displaystyle k =\frac{KE}{AC}=\frac{BP}{BO}\\ \\\frac{11,25-a}{21}=\frac{8-a}{8}\\ \\ 90-8a=168-21a\\\\13a=78\;\;\;\;\;|:13\\\\a=6$

МК = ЕН = 6 см;       КЕ = МН = 11, 25 = 6 = 5,21 (см)

#SPJ1