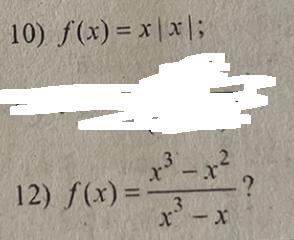Ответы
Ответ дал:
1
Ответ:
10) Непарная
12) Ни парная, ни не парная
Объяснение:
10) f(x) = x|x|
f`(x) =
f`(x) = x²
f`(x) =
f`(x) = 2x
Функция непарная (нечетная), так как:
f(-x)=-x·|x|
f(-x)=-f(x)
12) f(x)=
f`(x)=
Используем формулу a²×b²=(a-b)(a+b):
f`(x) =
Сокращаем общ. делитель Х:
f`(x) =
Сокращаем на общ. делитель х-1:
f`(x) =
Исп. правило дифференцирования:
f`(x) =
Упрощаем выражение:
f`(x) =
Функция ни четная, ни нечетная (ни парная, ни не парная), так как подставив х=-х, f(-x)≠f(x) и f(-x)≠-f(x)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад