Question

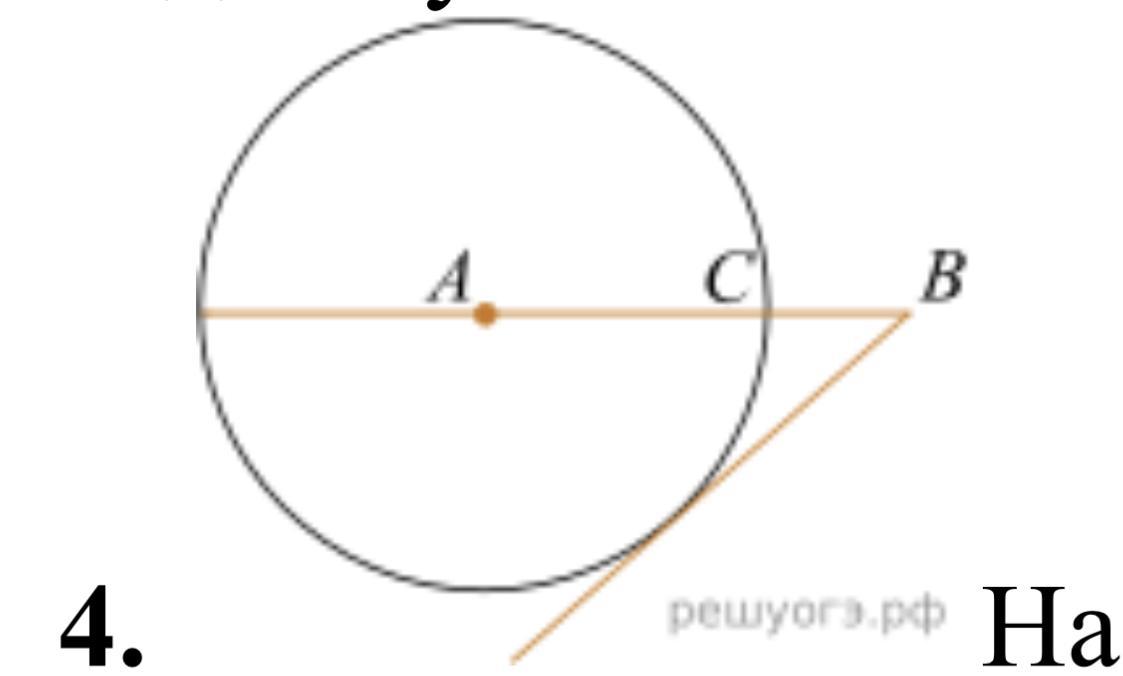
На отрезке AB выбрана точка C так, что AC=68 и BC=17. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Помогите пожалуйста

Answer 1

Ответ:

BD=51

Объяснение:

Знак перпендикулярности, буду обозначать как «T»

Дано:

окр(А, r); AC=68, BC=17; ВD–касательная, D–точка касания

Найти:BD–?

Решение:

Проведём AD T BD(св-во касательной "Касательная перпендикулярна к радиусу, проведённому в точку касания")

=>∆ABD:угол D=90°

AB=AC=68(т.к радиус)

AB=AC+BC=68+17=85

AB²=AC²+BD²

BD=√85²–68²=√(85-68) (85+68=√17*151=√2601=51

Ответ:BD=51