Question

Найти площадь фигуры, ограниченной указанными линиями.
Сделать чертёж.

y=1/3(x+2)^2, 3y -3x -16=0

Answer 1

Ответ:   19 1/18 кв.ед.

Объяснение:

y=1/3(x+2)^2;

3y -3x -16=0 =>  y=x+16/3

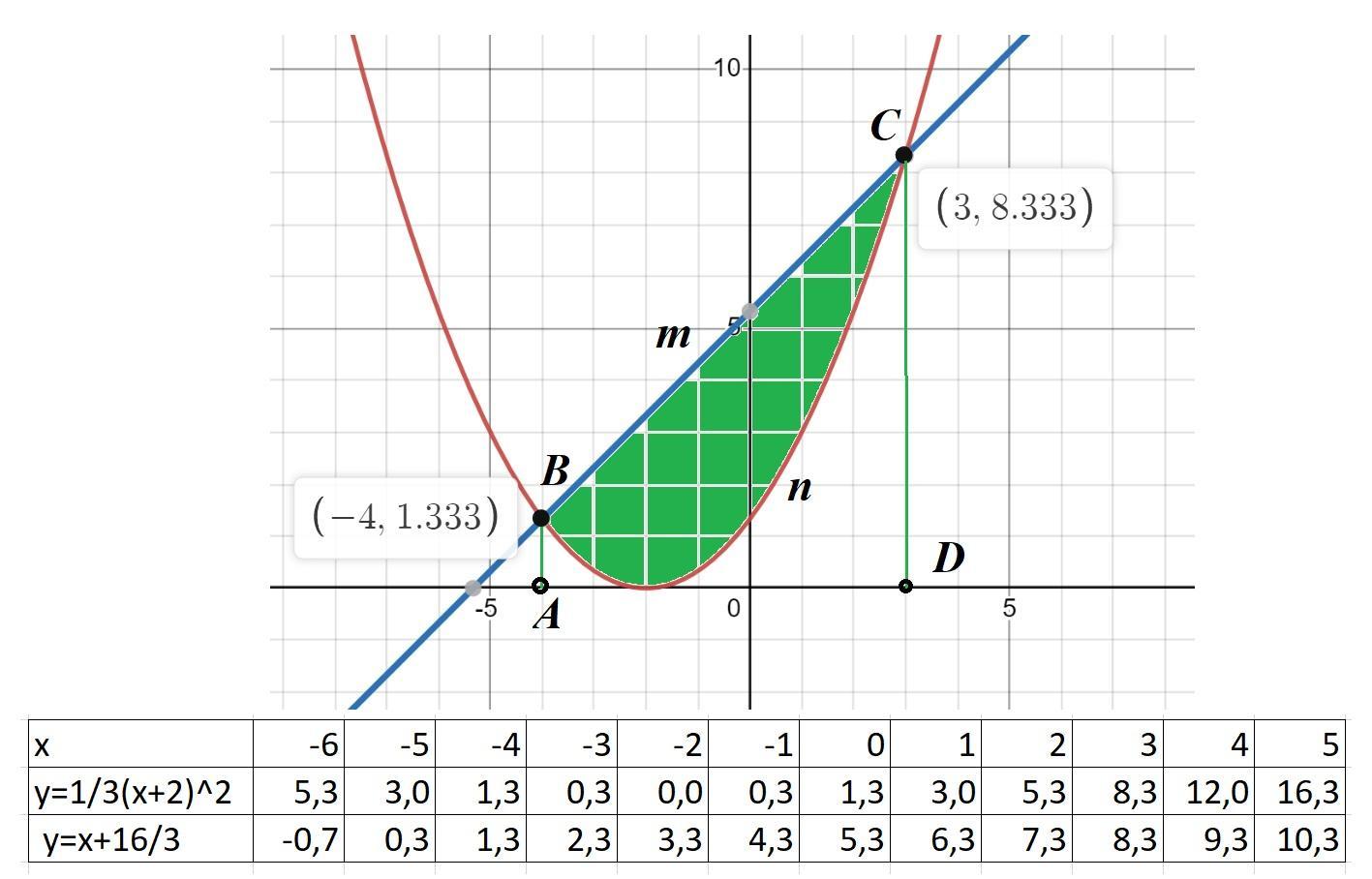
1)  Строим графики функций

2) Находим     по формуле Ньютона -Лейбница      S(ABmCD) - S(ABnCD) = ∫ₐᵇf₁(x)dx - ∫ₐᵇf₂(x)dx.

3)  пределы интегрирования (a;b) находим  по графику а=-4; b=3.

4) ∫₋₄³(x+16/3)dx - ∫₋₄³(1/3(x+2)^2)dx;

5)   ∫₋₄³(x+16/3)dx=x²/2|₋₄³ + 16/3x|₋₄³ = 1/2(9-16) + 16/3(3-(-4)) =

= -7/2 + 16*7/3 = -7/2 + 112/3 = 203/6.

6)  ∫₋₄³(1/3(x+2)^2)dx = 1/3∫₋₄³(x+2)²dx = 1/3*(x+2)³/3|₋₄³ =

=1/9 (3+2)³-(-4+2)³=1/9(125-(-8)) = 133/9.

7)   ∫₋₄³(x+16/3)dx-∫₋₄³(1/3(x+2)^2)dx=203/6-133/9=343/18 = 19 1/18 кв.ед.