Question

Площа трикутника ABC дорівнює 12 см². Чому дорівнює площа паралелограма,
три вершини якого збігаються з вершинами даного трикутника.

Answer 1

Ответ:

Площа паралелограма доорівнює 24 см²

Объяснение:

Площа трикутника ABC дорівнює 12 см². Чому дорівнює площа паралелограма, три вершини якого збігаються з вершинами даного трикутника.

Нехай АВС - даний трикутник. За умовою його площа становить

S₁=12 cм₂.

Три вершини трикутника збігаються з вершинами паралелограма.

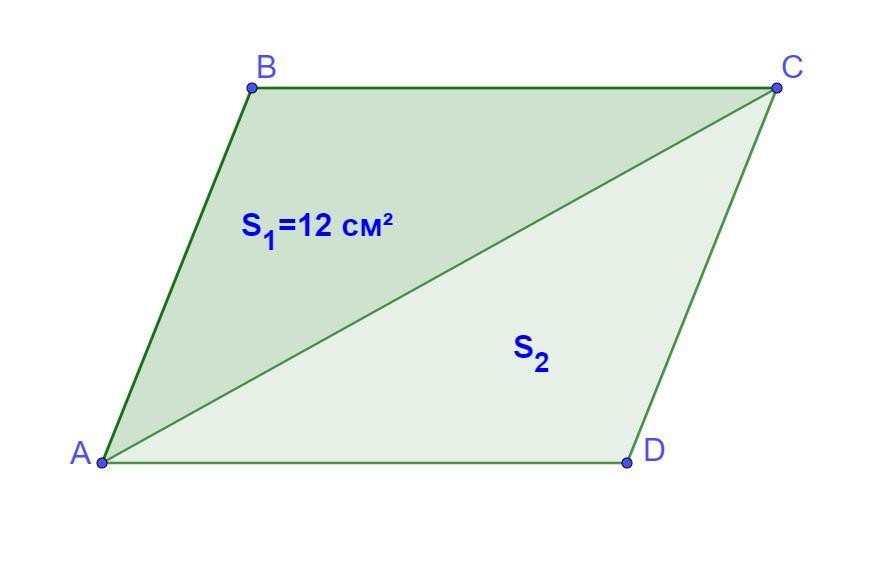
Добудуюмо трикутник до паралелограма. Для цьго проведемо CD║AB i AD║BC.

• Паралелограмом називають чотирикутник у якого протилежні сторони паралельні між собою.

Отже ABCD - паралелограм. АС - діагональ ABCD

За властивістю паралелограма: кожна з діагоналей паралелограма ділять його на два однакові за площею трикутники.

Тому S₂=S₁=12 cм²

Тоді площа паралелограма:

S(ABCD)=S₁+S₂=12+12=24 (см²)

Відповідь: 24 (см²)

#SPJ1