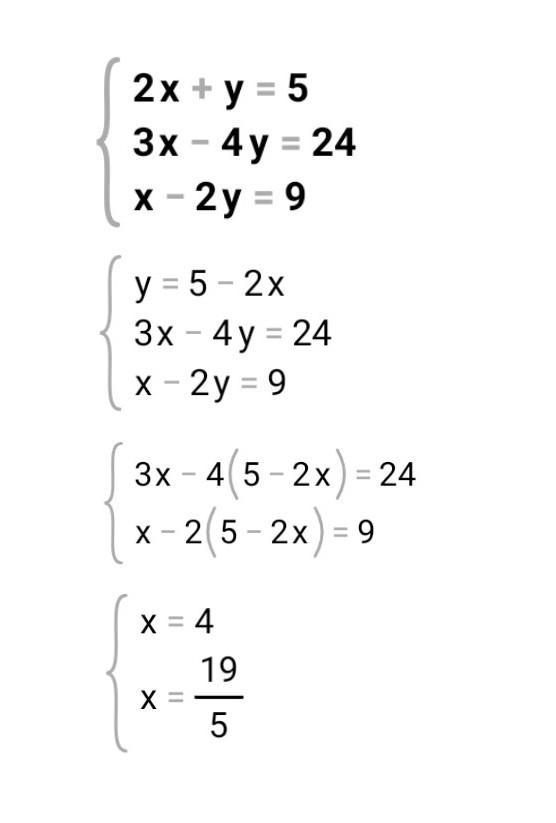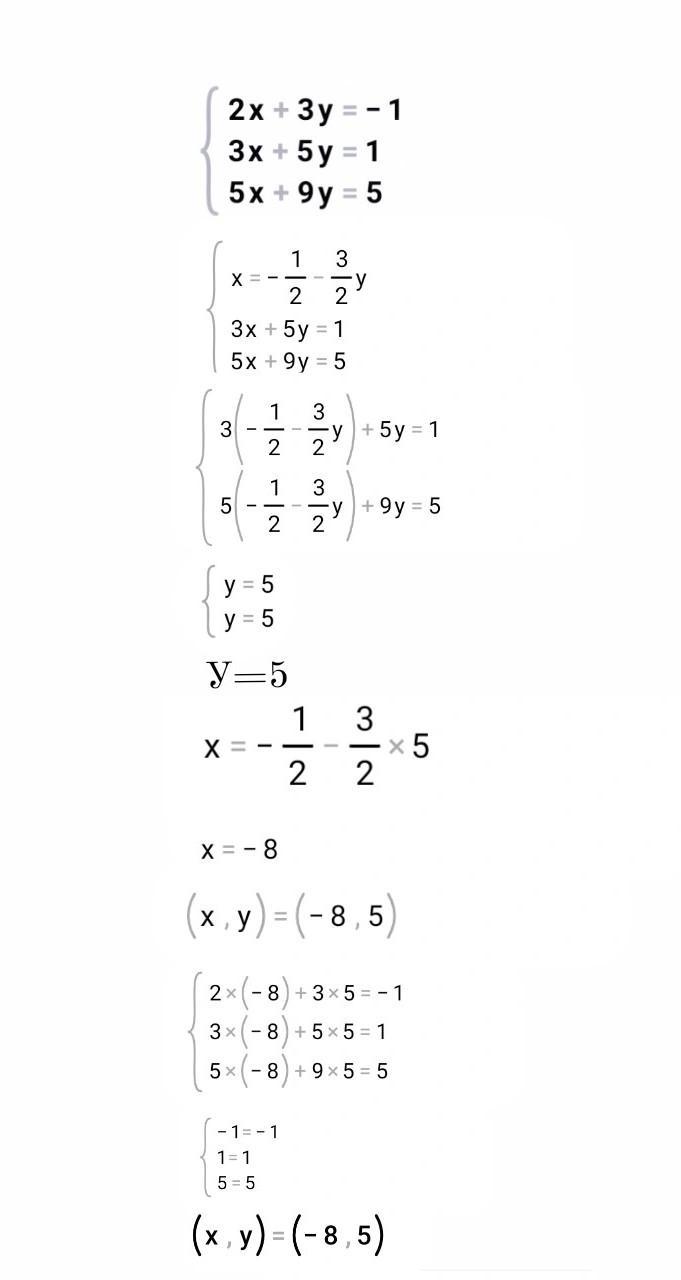Решите систему уравнений
1) 2x+ y = 5
3x - 4 y = 24
X - 2y = 9
2) 2x+ 3y = -1
3x + 5y = 1
5x + 9y = 5
До утра! Даю 65 баллов!
Ответы
Ответ:
1) Щоб розв'язати цю систему, ми можемо використати метод елімінації:
Множимо перше рівняння на 2, а друге на 3, і додаємо їх:
4x + 2y = 10
9x - 12y = 72
Знову множимо перше рівняння на 1 і додаємо до третього рівняння:
x - 2y = 9
4x = 19
x = 19/4
Підставляємо x у перше рівняння і знаходимо y:
2(19/4) + y = 5
y = -3/4
Таким чином, розв'язок системи рівнянь буде x = 19/4, y = -3/4.
2) Множимо перше рівняння на 3 і віднімаємо від другого:
2x + 3y = -1
-4x - 4y = 4
Тепер множимо перше рівняння на 5 і віднімаємо від третього:
10x + 15y = -5
-4x - 4y = 4
Отримали систему:
-4x - 4y = 4
10x + 15y = -5
Множимо перше рівняння на -5/4:
x + y = -1
Підставляємо x + y в друге рівняння:
10x + 15y = -5
10(x + y) = -5
x + y = -1/2
Отже, ми отримали систему:
x + y = -1/2
x + y = -1
Ця система не має розв'язку, оскільки дві лінії паралельні і не перетинаються.
Объяснение:
Ответ:
Ответ на фото:⬆️⬆️⬆️⬆️⬆️⬆️⬆️⬆️