Question

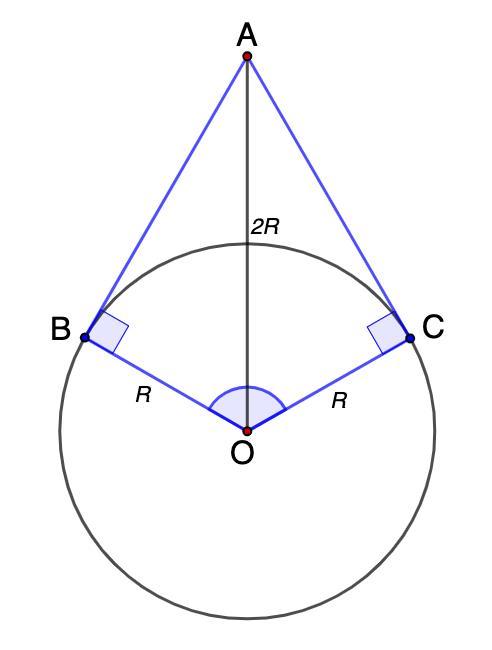
К окружности с центром в точке О провели две касательные АВ и АС из точки А так, что В и С - точки касания. Определите
градусную меру центрального угла, опирающегося на меньшую дугу ВС, если известно,что длина отрезка АО равна диаметру
данной окружности.
Можно пожалуйста с рисунком и желательно с «дано»

Answer 1

Ответ:

Градусная мера центрального угла, опирающегося на меньшую дугу ВС равна 120°

Объяснение:

К окружности с центром в точке О провели две касательные АВ и АС из точки А так, что В и С - точки касания. Определите градусную меру центрального угла, опирающегося на меньшую дугу ВС, если известно, что длина отрезка АО равна диаметру данной окружности.

Дано: Окр.(О,R);

AB, AC - касательные;

АО = d - диаметру окружности;

Найти: ∠ВАС

Решение:

Проведем радиусы ОВ и ОС.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОВ ⊥ АВ; ОС ⊥ АС.

Рассмотрим ΔВАО - прямоугольный.

АО = d

• Диаметр равен двум радиусам.

⇒ АО = 2R; OB = R

• Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то он лежит против угла в 30°.

⇒ ∠ВАО = 30°

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ∠ВАО = ∠ОАС = 30°   ⇒ ∠А = 60°

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠ВОС =  ◡ВС.

Угол между двумя касательными равен 180° минус градусная мера дуги, заключенной внутри него.

⇒  ∠А = 180° - ◡ВС   или   ∠А = 180° - ∠ВОС

60° = 180° - ∠ВОС

∠ВОС = 120°

Градусная мера центрального угла, опирающегося на меньшую дугу ВС равна 120°.

#SPJ1