Ответы
Ответ дал:
1
Ответ: 126°.
Объяснение:
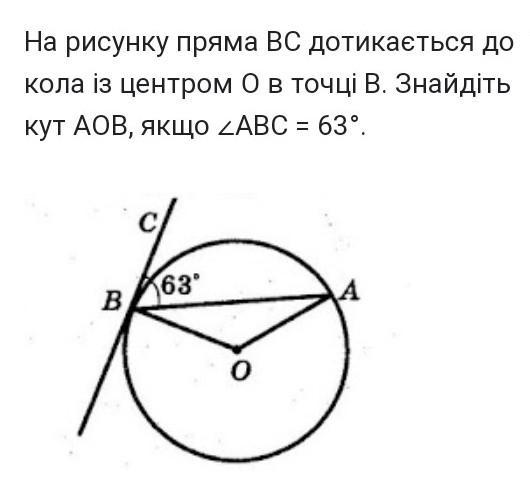
Известно, что радиус окружности перпендикулярен касательной. Следовательно, ∠СВО = 90°.
∠ABO=∠CBO-∠CBA =90°-63° = 27°.
Треугольник AOB равнобедренный ОВ=ОА=R. Поэтому углы при основании АВ равны => ∠ABO=∠BAO = 27°.
Сумма углов треугольника равны 180°. Тогда
∠АОВ = 180°-2*27° = 180°-54° = 126°.
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад