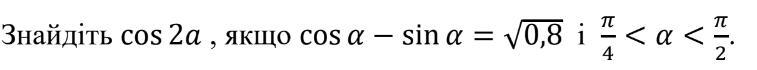Question

СРОЧНО ДАЮ 100 БАЛАВ
Знайдіть cos 2a , якщо cos α − sin α = √0,8 і π4 < α < π2

Answer 1

Ответ:

За тригонометричним тотожностями, ми знаємо, що:

cos(2a) = cos^2(a) - sin^2(a)

Ми можемо використати формули Ейлера для заміни тригонометричних функцій через комплексні експоненти:

cos(a) = (e^(ia) + e^(-ia))/2

sin(a) = (e^(ia) - e^(-ia))/2i

Таким чином, ми можемо замінити cos(α) та sin(α) за їх експонентними формами:

cos(α) - sin(α) = √0.8

(e^(iα) + e^(-iα))/2 - (e^(iα) - e^(-iα))/2i = √0.8

Множимо обидві сторони на 2i, щоб позбутися від знаменника від'ємного імагінарного доданку:

i(e^(iα) + e^(-iα)) - (e^(iα) - e^(-iα)) = 2i√0.8

Знайдемо суму експонент, використовуючи формулу Ейлера:

i(2cos(α)) - 2isin(α) = 2i√0.8

Розділимо обидві частини на 2i:

cos(α) - sin(α) = √0.8

sin(α) = cos(α) - √0.8

Тепер ми можемо знайти cos(2α), використовуючи формулу зверху:

cos(2α) = cos^2(α) - sin^2(α) = cos^2(α) - (cos(α) - √0.8)^2

Замінюємо cos(α) за попереднім результатом:

cos(2α) = (1 - √0.8)^2 - (1 - √0.8 - √0.8)^2

Обчислюємо:

cos(2α) = 0.36 - 0.64 = -0.28

Отже, cos(2α) = -0.28

Answer 2

Можемо скористатися формулою подвійного кута для косинуса: cos 2a = cos^2 a - sin^2 a.

З формули тригонометричних співвідношень для кута α, маємо:

cos α = √0,8 / 2 = 0,4472,
sin α = cos α - √0,8 = 0,4472 - 0,8944 = -0,4472 (бо π/4 < α < π/2, тобто sin α < 0).

Тоді можна знайти:

cos^2 α = 0,8 / 4 = 0,2,
sin^2 α = (-0,4472)^2 = 0,2.

Застосовуючи формулу для косинуса подвійного кута, отримуємо:

cos 2α = cos^2 α - sin^2 α = 0,2 - 0,2 = 0.

Отже, cos 2a дорівнює 0.