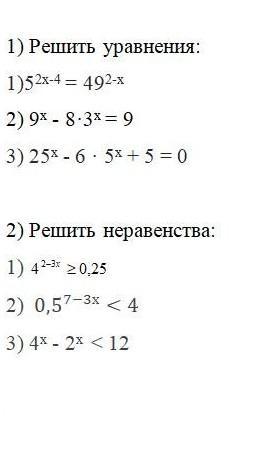Question

помогите решить все 2 задачи ​

Answer 1

Ответ:

1.1) x = 2

1.2) x = 2

1.3) x = 0;1

2.1) x ≤ 1

2.2) x < 3

2.3) x < 2

Пошаговое объяснение:

1) Решить уравнения:

1)

$5^{2x-4}=49^{2-x}\\5^{2x-4}=(7^2)^{2-x}\\5^{2x-4}=7^{4-2x}\\5^{2x-4}=7^{-1(2x-4)}\\5^{2x-4}=(7^{-1})^{2x-4}\\5^{2x-4}=(\frac{1}{7} )^{2x-4$

Так как показатели у нас одинаковые, а основания - разные, то равенство достигается только тогда, когда оба показателя равны 0:

$2x-4=0\\\boxed{x=2}$

2)

$9^x-8*3^x=9\\(3^2)^x-8*3^x-9=0\\(3^{x})^2-8*3^x-9=0$

Введем новую переменную $t=3^x$:

$t^2-8t-9=0\\t^2+t-9t-9=0\\t(t+1)-9(t+1)=0\\(t-9)(t+1)=0\\t=-1;9$

Обратная замена:

1. $3^x=-1$

  Корней нет, так как t должно быть > 0.

2. $3^x=9$

   $3^x=3^2\\\boxed{x=2}$

3)

$25^x-6*5^x+5=0\\(5^x)^2-6*5^x+5=0$

Введем новую переменную $t=5^x$:

$t^2-6t+5=0\\t^2-t-5t+5=0\\t(t-1)-5(t-1)=0\\(t-5)(t-1)=0\\t=1;5$

Обратная замена:

1. $5^x=1$

  $5^x=5^0\\\boxed{x=0}$

2. $5^x=5$

   $5^x=5^1\\\boxed{x=1}$

2) Решить неравенства:

1)

$4^{2-3x}\geq 0.25\\\frac{4^2}{4^{3x}} \geq 0.25\\\frac{16}{0.25} \geq 4^{3x}\\64\geq 4^{3x}\\4^3\geq 4^{3x}$

Основания равны, поэтому будем работать с показателями:

$3\geq 3x\\\boxed{x\leq 1}$

2)

$0.5^{7-3x} < 4\\(2^{-1})^{7-3x} < 2^2\\2^{3x-7} < 2^2$

Основания равны, работаем с показателями:

$3x-7 < 2\\3x < 9\\\boxed{x < 3}$

3)

$4^x-2^x < 12\\(2^x)^2-2^x-12 < 0$

Введем новую переменную $t=2^x$:

$t^2-t-12 < 0\\t^2+3t-4t-12 < 0\\t(t+3)-4(t+3) < 0\\(t-4)(t+3) < 0$

t ∈ (-3; 4)

Обратная замена:

$\left \{ {{2^x > -3} \atop {2^x < 4}} \right. \\\left \{ {{x=R} \atop {x < 2}} \right. \\\boxed{x < 2}$