СРОЧНО
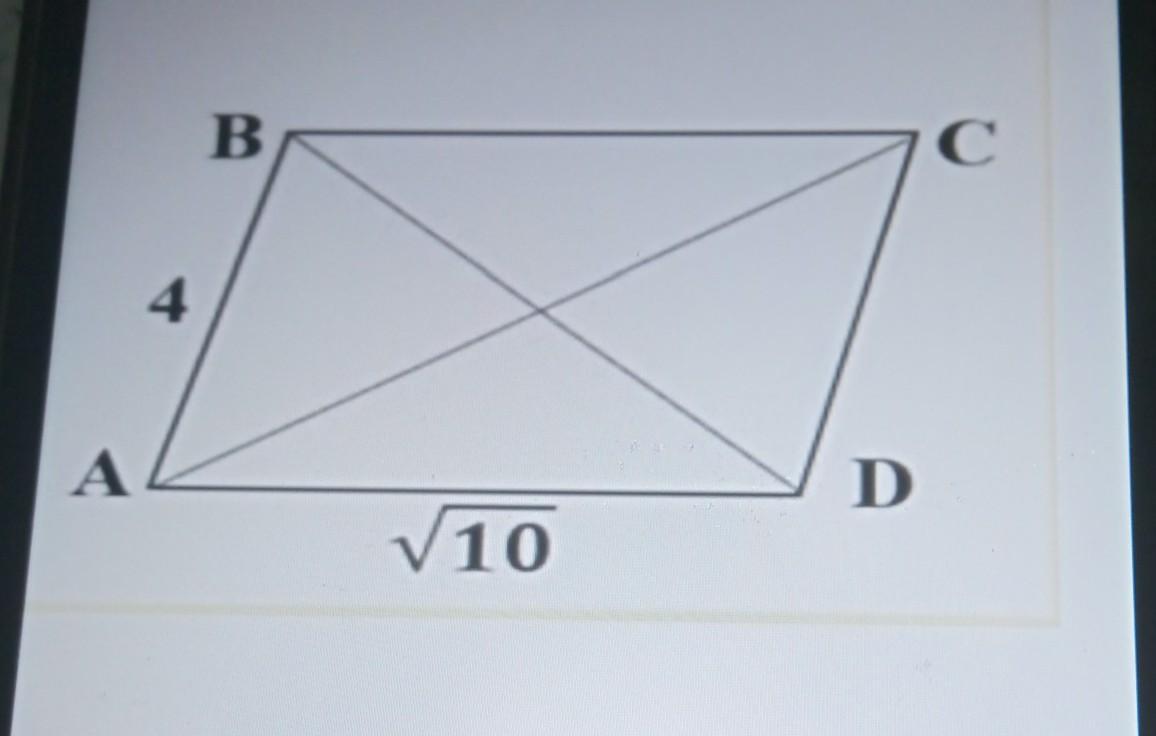
одна зі сторін паралелограма на 2 см більша за іншу, сторони паралелограма дорівнюють 4 і √10. знайдіть діагоналі паралелограма.
Ответы
Ответ:
Оскільки паралелограм має протилежні сторони, які паралельні і рівні за довжиною, то його сторони можуть бути позначені як AB = 4 і DC = √10, де AB || DC і AB = DC.
Також з умови задачі відомо, що одна зі сторін паралелограма (наприклад, AB) на 2 см більша за іншу (наприклад, BC). Оскільки протилежні сторони паралелограма мають однакову довжину, то сторона BC має довжину 4 - 2 = 2 см.
Для знаходження діагоналей паралелограма можна використати теорему Піфагора для прямокутного трикутника. Нехай AC та BD - діагоналі паралелограма. Оскільки AC і BD перетинаються в точці E і поділяються ним на дві рівні частини, то AE = EC і BE = ED.
Розглянемо трикутник AEB. Застосовуючи теорему Піфагора, отримуємо:
BE² = AB² + AE²
BE² = 4² + (DC / 2)²
BE² = 16 + 5
BE = √21
Тепер розглянемо трикутник CED. Знову застосовуючи теорему Піфагора, отримуємо:
CE² = CD² + DE²
CE² = (AB - BC)² + AE²
CE² = (4 - 2)² + (DC / 2)²
CE² = 2² + 5
CE = √9
CE = 3
Отже, діагоналі паралелограма мають довжини √21 та 3.