Ответы
Відповідь:
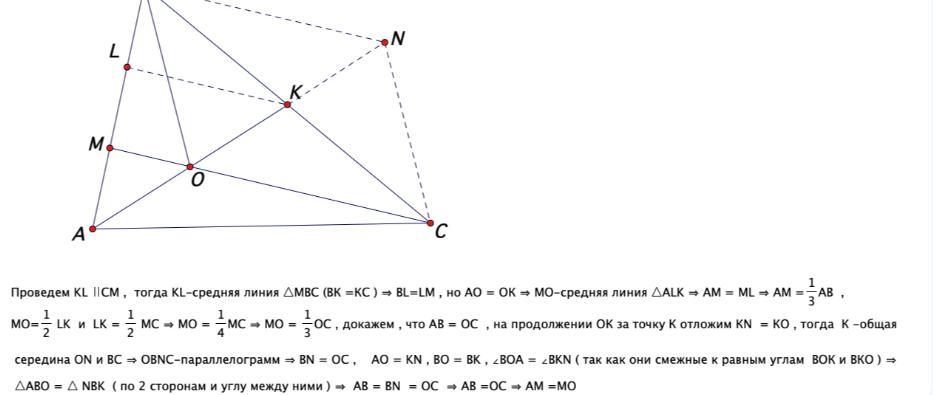
168) на фото
169) Для доведення того, що точка O - центр описаного кола трикутника ABC, ми повинні показати, що відстані від точки O до кожної з трьох вершин трикутника ABC є однаковими, тобто що OA = OB = OC, де A, B і C - вершини трикутника.
Оскільки точка O знаходиться на серединному перпендикулярі до сторони AC, то вона знаходиться на рівній відстані від вершин A і C. Оскільки також OC = AB, то ми можемо скористатися тим, що відрізок, який з'єднує середини двох сторін трикутника, ділиться ним на дві рівні частини. Таким чином, ми можемо сказати, що точка O знаходиться на рівній відстані від вершин B і C.
Отже, ми маємо OA = OC і OB = OC, що означає, що точка O знаходиться на рівній відстані від кожної з трьох вершин трикутника. Тому точка O є центром описаного кола трикутника ABC.
170) Высота равностороннего треугольника равна а√3/2, где а-сторона треугольника, а радиус, вписанный в этот треугольник составляет треть высоты, т.е. а√3/6=8⇒а=48/√3=16√3/см/
Значит, высота 16√3*√3/2=24/см/
Задачу можно решить короче, в одно действие, если вспомнить, что высота равностороннего треугольника состоит из трех радиусов, вписанных в окружность этого треугольника, т.е. 3*8=24/см/