Question

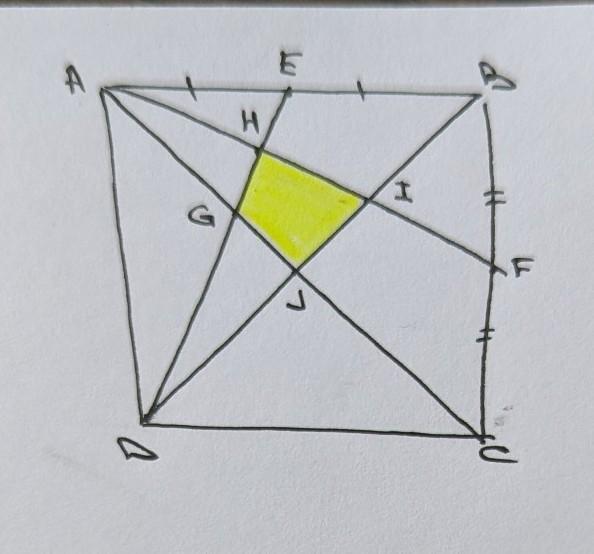
найти площадь фигуры GHIJ, если известно, что
ABCD - квадрат
AE = EB
BF = FC
площадь квадрата
S_ABCD = 1​

Answer 1

Ответ:

S(GHIJ) = 0,05 (ед)²

Объяснение:

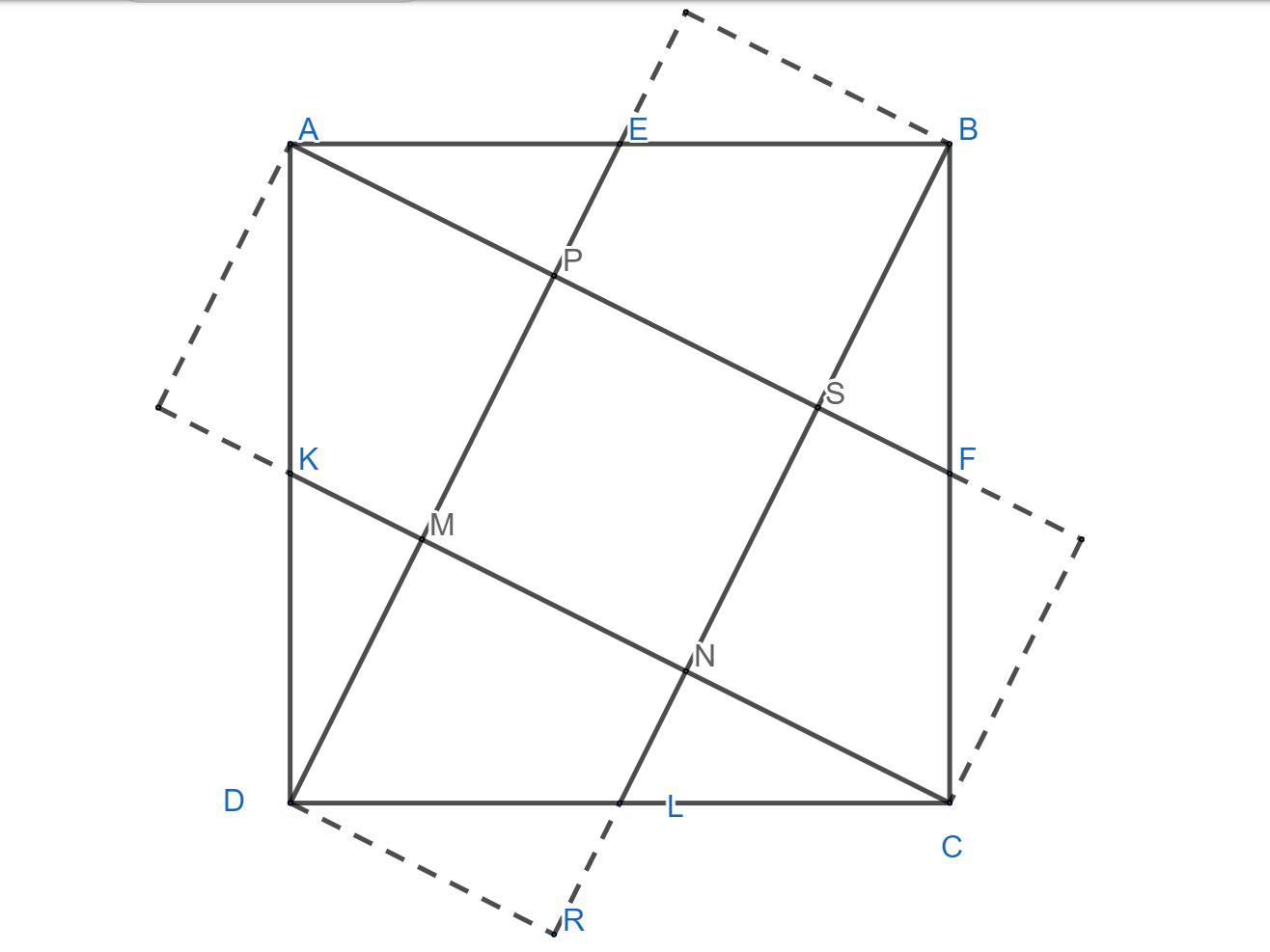
Рисунок № 1

Рассмотрим квадрат ABCD ,   проведем отрезки  AF, KC , DE , BL  
( E,F,L,K - середины сторон квадрата )  на пересечениях этих отрезков будет располагаться MPSN

Очевидно , что за счет симметрии треугольники AEP ,  BSF , NLC , DKM имеют равные площади  

Тоже самое и  с четырехугольниками  PMKA , BSPE , NSFC , NLDM

Теперь заметим , что если на продолжение  BL с точки D провести перпендикуляр ,  образуется ΔDRL    который  будет доводить  NLDM до квадрата ,   а поскольку  ΔDRL и ΔLNC равные ,  то объединив площадь NLDM с площадью  LNC  образуется квадрат DMNR который равен квадрату MPSN ,  повторяя аналогичное с отрезками AF, KC , DE , мы можем понять что каждый четырехугольник мы можем довести до квадрата.  Таких квадратов будет  четыре  ,  а  у с учетом MPSN пять

Их суммарная площадь равна площади квадрата ABCD  , т.е

5S  = 1

S = 0.2 ед² ⇒ площадь MPSN  равна 0.2 ед²

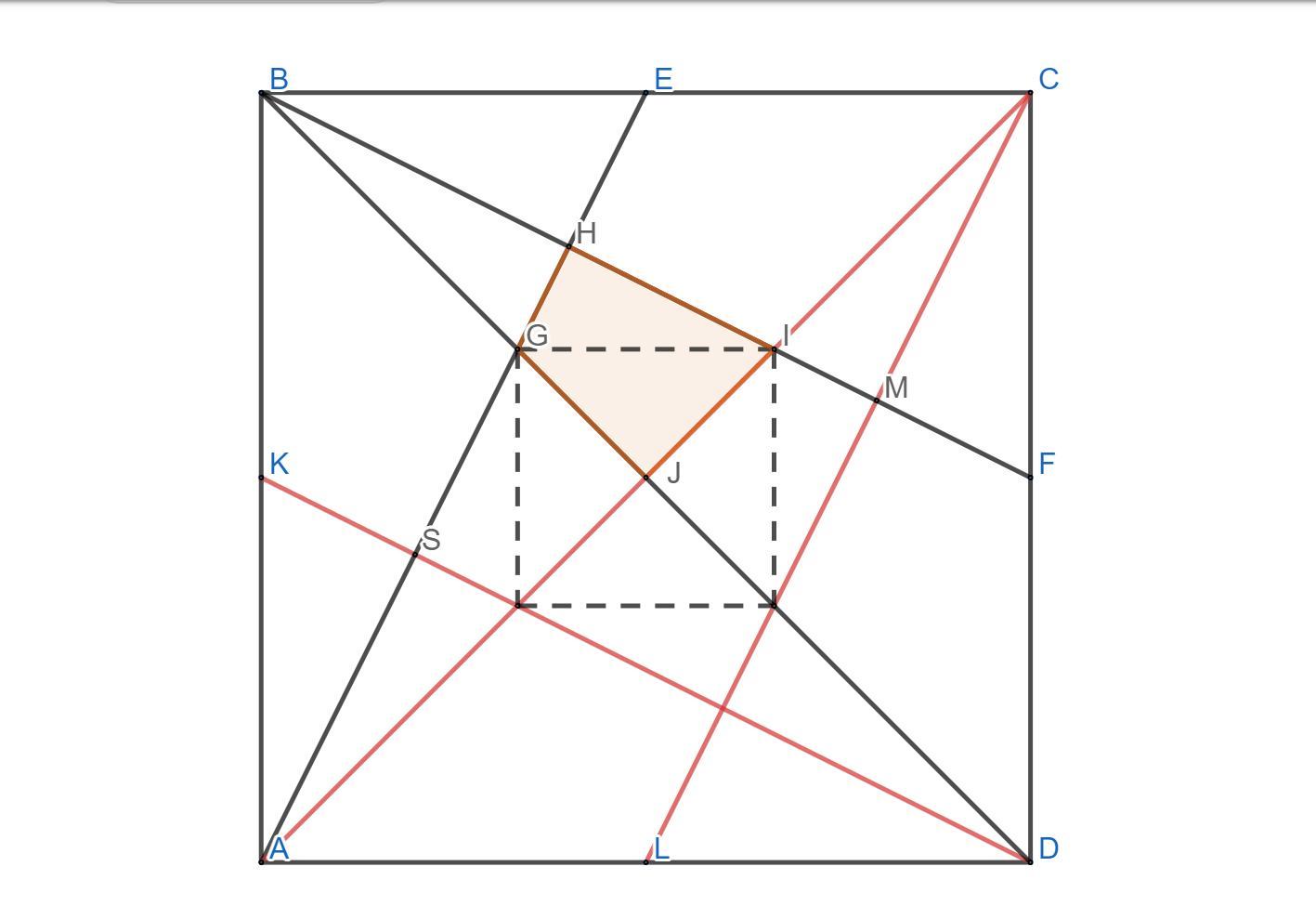
Рисунок №2

Теперь вернемся к нашей исходной задаче , проведем  DK,AC,CL
Из 2-го рисунка мы знаем что площадь центрального квадрата  (MPSN рис №1) равна  0,2 ед² ,  теперь же проведенные диагонали разобьют его на четыре равных четырехугольника среди которых есть GHIJ , соответственно его площадь будет равна  1/4 площади  квадрата MPSN , т.е  

Площадь GHIJ  равна  

$\dfrac{1}{4}\cdot 0,2 = 0, 0 5$ (ед)²