Question

Угол между высотой и диагональю, проведенными из вершины тупого угла, равен
54 0 . Найди углы ромба. Сделай рисунок.

Answer 1

Решение.

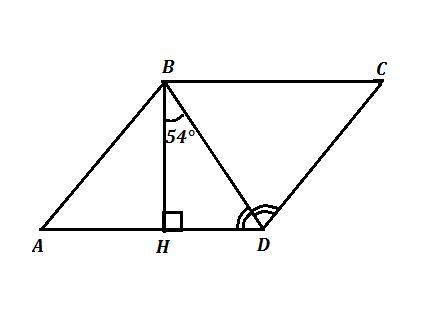
Угол  между высотой и диагональю, проведенными из вершины тупого угла, равен 54° .  Найти углы ромба .

ABCD - ромб .  ВН ⊥ AD , ∠DBH=54°

Рассмотрим ΔDBH . Он прямоугольный . Сумма острых  углов прямоугольного треугольника равна 90° .  Поэтому

∠BDH = 90°-∠DBH = 90° - 54° = 36°

Диагонали ромба являются биссектрисами его углов, поэтому  

∠АDC = 2 *∠DBH = 2 * 36° = 72°  

Противоположные углы ромба равны между собой . Поэтому

∠АВС=∠ADC = 72°  

∠BAD = ∠BCD = 180°- 72° = 108°  

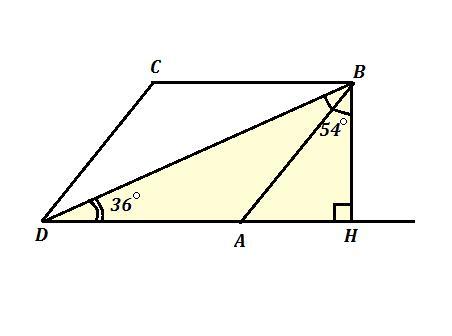
Замечание . Получается, что в условии написали, что высота и диагональ проведены из тупого угла, а на самом деле из острого . Смотри рисунок 2 .