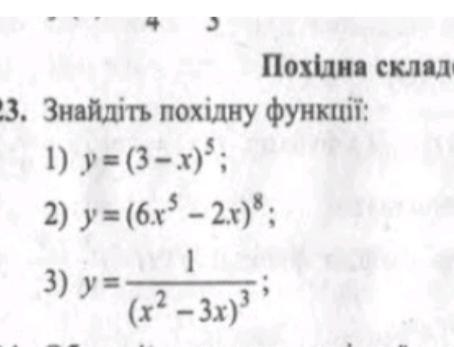Ответы
Ответ дал:
0
Пояснення:
Ответ дал:
0
Ответ:
Формула производной степенной функции : ,
где - внутренняя функция .
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад