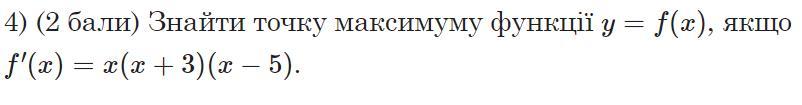Ответы
Ответ дал:
1
Ответ:
Точки экстремума функции могут быть в критических точках , где производная равна 0 или не существует .
Расставим знаки производной на промежутках .
Точка максимума функции будет в той точке , при переходе через которую производная меняет знак с плюса на минус .
iorbko:
супер)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад