Моторний човен пройшов 60 км за течією річки і 36 км озером,витративши на весь шлях 5 год. Знайдіть власну швидкість човна,якщо швидкість течії 2 км/год.
Ответы
Ответ дал:
1
Ответ:
Скорость лодки равна х км/ч .
Скорость лодки по течению реки равна (х+2) км/ч .
Прошла лодка по течению реки 60 км за t₁ = 60/(х+2) часа .
Лодка прошла по озеру 36 км за t₂ = 36/х часа .
На прохождение всего пути потрачено t₁+t₂=5 часов .
Составим уравнение .
Первое число отрицательное, и не подходит по смыслу задачи . Поэтому выбираем второе число .
Ответ: собственной скорости моторной лодки 18 км\ч .
Приложения:
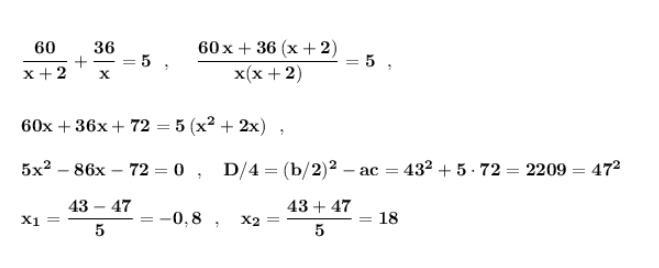
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад