Ответы
Ответ дал:
1
Відповідь:Використовуючи властивості логарифмів, можна скористатися формулою заміни основи:
log a b = log c b / log c a,
де a, b, c - дійсні числа, a ≠ 1, b > 0, c > 0, c ≠ 1.
Тоді:
log3 4 = log10 4 / log10 3
log4 5 = log10 5 / log10 4
log5 7 = log10 7 / log10 5
log7 81 = log10 81 / log10 7
Замінюємо значення логарифмів:
log3 4 • log4 5 • log5 7 • log7 81 = (log10 4 / log10 3) • (log10 5 / log10 4) • (log10 7 / log10 5) • (log10 81 / log10 7)
Після спрощення багатьох дробів, отримаємо:
log3 4 • log4 5 • log5 7 • log7 81 = log10 81 / log10 3 = log3 81 = 4.
Покрокове пояснення:
Ответ дал:
0
я тебе помогла не ну ето легко а моя задача тижёлая как ето????
Приложения:
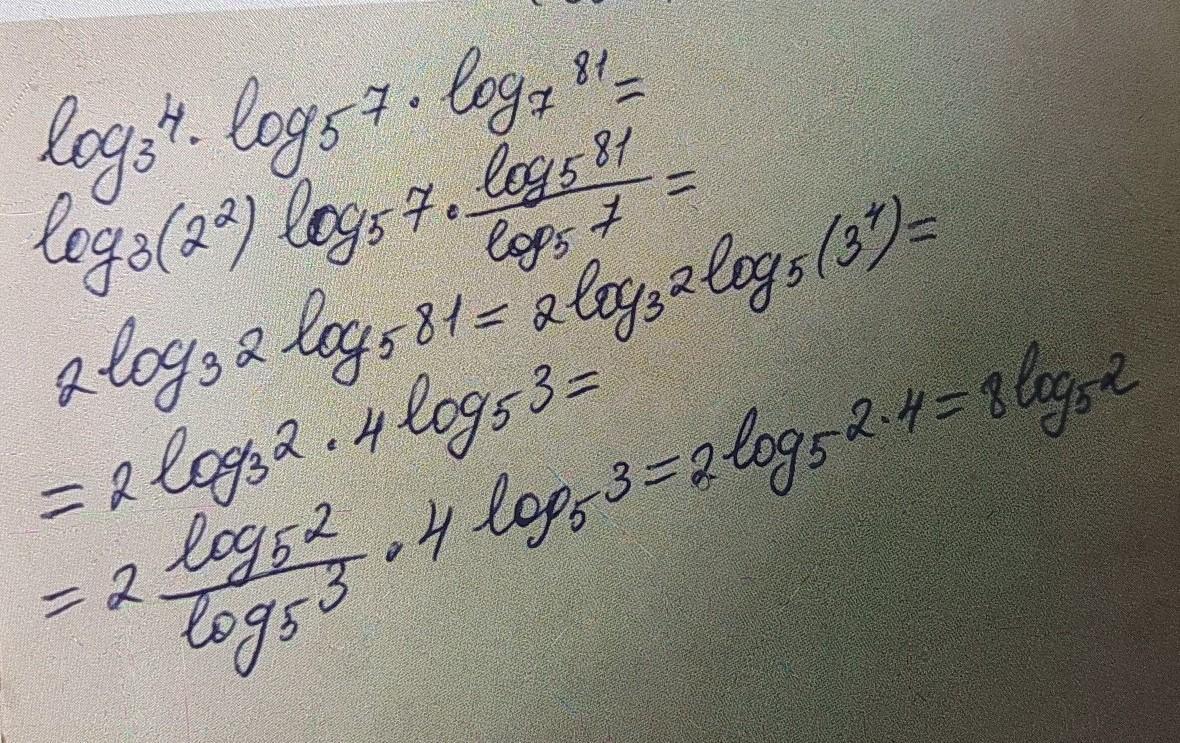
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад