Question

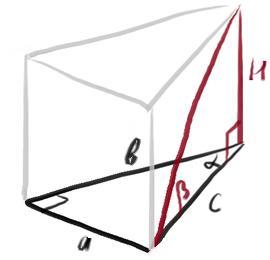
В основі прямої призми лежить прямокутний трикутник з гострим кутом а(альфа) i гіпотенузою с.

Якщо діагональ бічної грані, що містить гіпотенузу основи, нахилена до площини основи під кутом в(бета), то об'єм призми дорівнює:

Answer 1

Объем прямой призмы  - произведение площади основания на высоту.

V = Sо H

a/c=sinA ; b/c=cosA

S△=1/2 ab =1/2 c^2 sinAcosA =1/4 c^2 sin(2A)

Боковые грани прямой призмы перпендикулярны основанию.

Следовательно, наклон диагонали боковой грани к основанию, это наклон к ребру основания.

Тогда из прямоугольного треугольника находим боковое ребро, которое в прямой призме равно высоте.

H/c =tgB => H =c tgB

V = Sо H =1/4 c^3 sin(2A) tgB