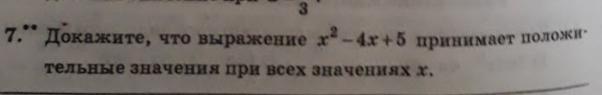Ответы
Ответ дал:
0
Ответ:
0
Объяснение:
докажите что выражение x^2-4х+5 принимает положительные значения при всех значениях X
Первый вариант
x^2-4x+5 =x^2-4x+4+1=(x-2)^2+1
так как квадрат разности (х-2)^2 >=0 при всех значениях х на числовой оси то сумма (x-2)^2+1>0 или принимает только положительные значения при всех значениях х Второй вариант
x^2-4х+5 =0
D=16-20=-4<0
Так как коэффициент при x^2 больше нуля (1>0) и дискриминант отрицателен, то гарфик параболы не имеет точек пересечения с осью Ох и находится выше оси Ох. Поэтому при любых значениях x x^2-4x+5>0
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад