Question

Срочно!При яких значення в і с вершина параболи у=4x²+bx+c знаходиться у точці B(3; 2)?​

Answer 1

Відповідь:

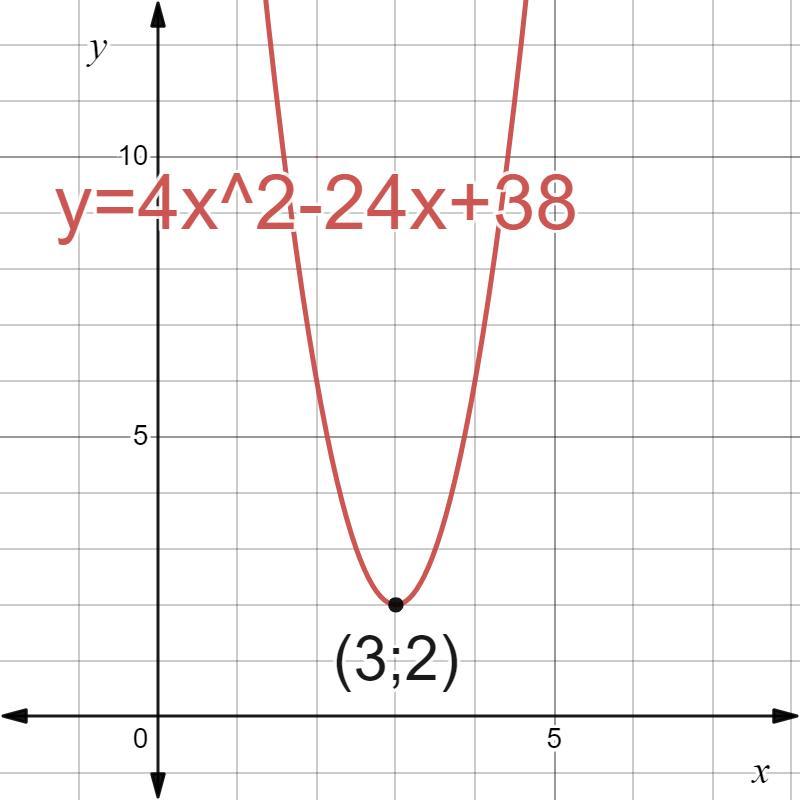
З погляду B(3; 2) накласти параболу у=4x²+bx+c, крім того, можна записати співвідношення: 2 = 4 3² + b 3 + c

Це дає першу рівність із двох змінних. Щоб дізнатися два невідомі і с, потрібна друга рівність. Можна висловити будь-яку в точці на параболі або додаткову умову. Якщо такої додаткової умови немає, то є безліч варіантів рішення.

Наприклад, припустимо, що вершина параболи перебуває у точці (0, c). В цьому випадку вершина максимально функціонує і розпізнаватиметься на серединних точках між B і (0, c), тобто на отворі 3/2 від кожної з цих точок. Таким чином, можна записати:

2 = 4 3² + b 3 + c c = 4 0² + b 0 + c

Оскільки, як правило, вершина розпізнається на виході з точки B, вона також розпізнається на виході з точки (6, 4 6 + 6 + c), а також з невеликою точкою на параболі. Тоді, використовуючи формулу поділу між точками, можна записати:

2 = 4*(3+p)² + b*(3+p) + c c = 4*(6-p)² + b*(6-p) + c

Отже, можна отримати систему двох рівнянь з двох невідомих b і c, яку можна вирішити для знаходження b і c.

Answer 2

Пояснення:

$\displaystyle\\y=4x^2+bx+c\ \ \ \ \ \ \Rightarrow\ \ \ \ a=4.\\\\B(3;2)\ \ \ \ \ \ x_B=3\ \ \ \ \ \ y_B=2.\\\\x_B=\frac{-b}{2a} \\\\3=\frac{-b}{2*4} =\frac{-b}{8}\ |*(-8) \\\\b=-24\\\\y_B=4x^2-24x+c\\\\2=4*3^2-24*3+c\\\\2=36-72+c\\\\c=38.$

Відповідь: b=-24,   c=38.