Ответы
Ответ дал:
3
Ответ: 8 ед²
Пошаговое объяснение:
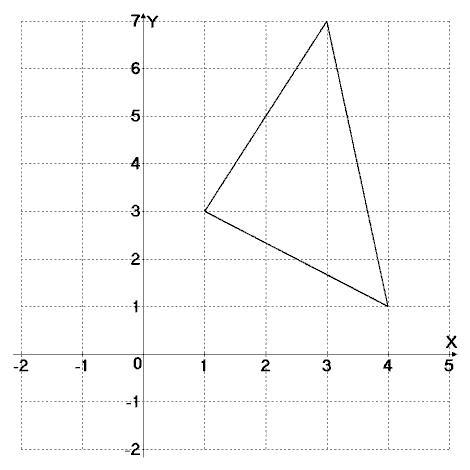
Для начала определим координаты вершин этого треугольника
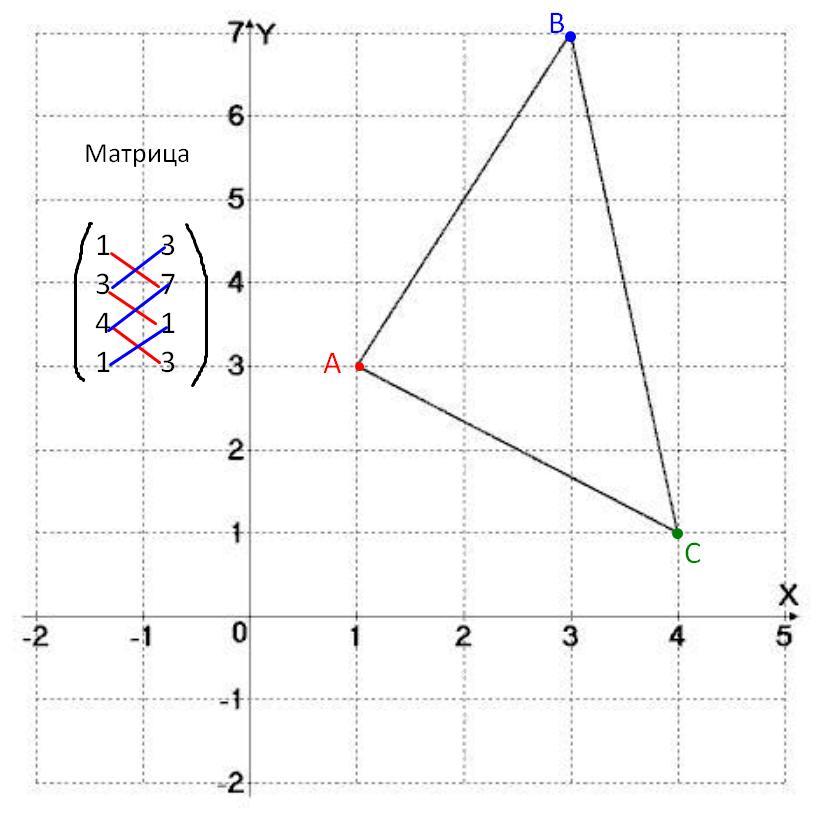
A (1 ; 3) , B(3 ; 7) , С(4 ; 1)
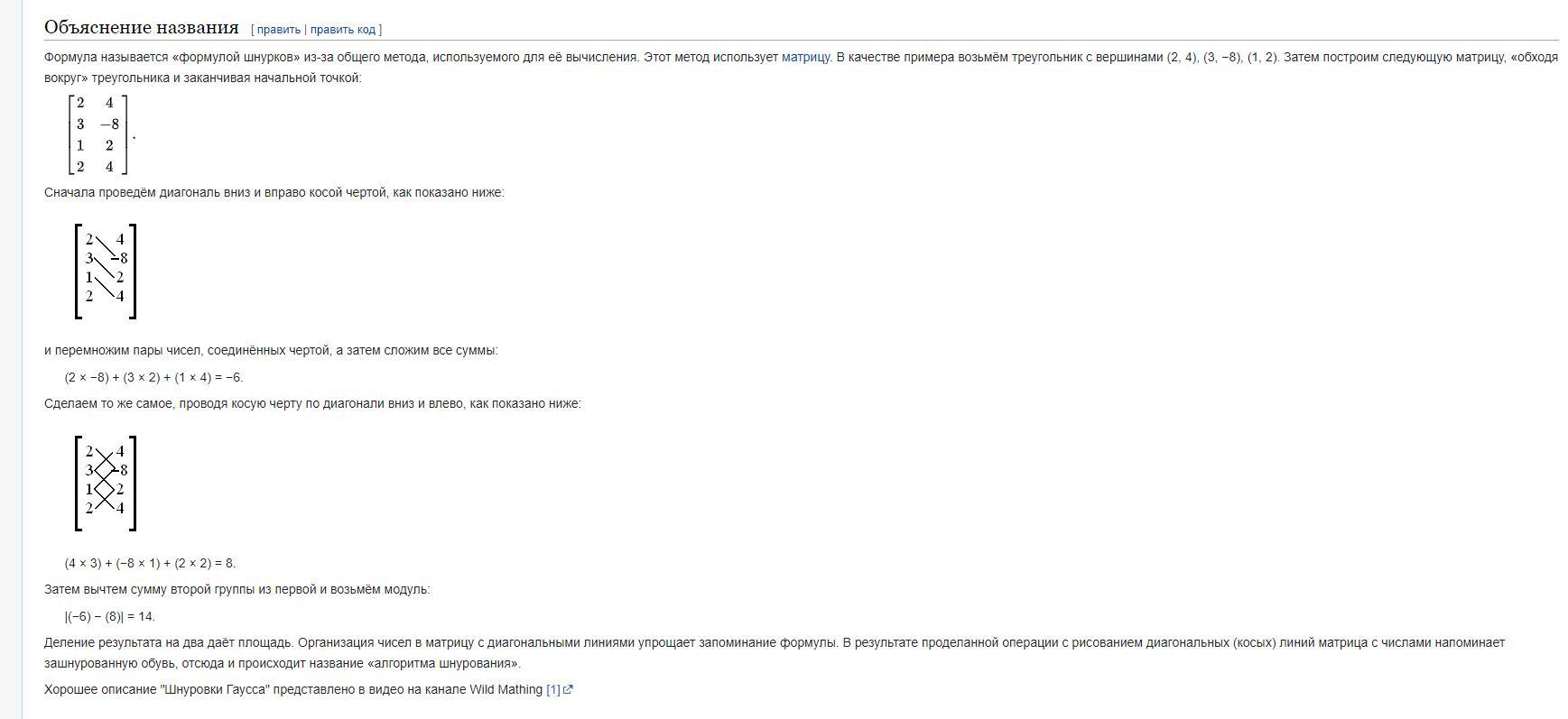
Воспользуемся как на мой взгляд , самой простой интерпретацией координатного метода нахождения площади треугольника , а именно Формулой Шнурков
Пусть A будет точкой с которой мы начнем , а далее составляем матрицу
Cумма произведений вдоль линий, проведенных от левого верхнего элемента к правому нижнему :
Δ₊ = 1·7 + 3·1 + 4·3 = 7 + 3 + 12 = 22
Cумма произведений вдоль линий, проведенных от правого верхнего элемента к левому нижнему :
Δ₋ = 3·3 + 4·7 + 1·1 = 9 + 28 + 1 = 38
Находим искомую площадь :
ед²
#SPJ1
Приложения:
ylianakononova1:
Не правильно.
Я получила 2!
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад