Алгебра. Даю 100 балів. потрібно вирішити завдання з максимальним поясненням щоб було усе зрозуміло будь ласка.
з дуже детальним поясненням будь ласка
Приложения:

Ответы
Ответ дал:
1
Ответ: 6,25 .
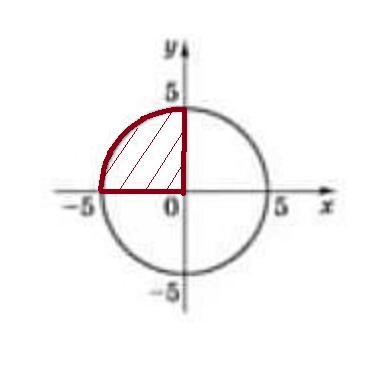
Уравнение окружности с центром в точке (0,0) и радиусом R=5 .
Выразим переменную у : .
Уравнение определяет нижнюю полуокружность , а
уравнение определяет верхнюю полуокружность .
С помощью интеграла
можно вычислить площадь области,
ограниченной верхней полуокружностью и прямыми х= -5 , х=0 и
у=0 . Но эту площадь можно вычислить как площадь четверти круга
с радиусом R=5 : .
Тогда вычислим значение заданного выражения :
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад