Question

Помогите пожалуйста
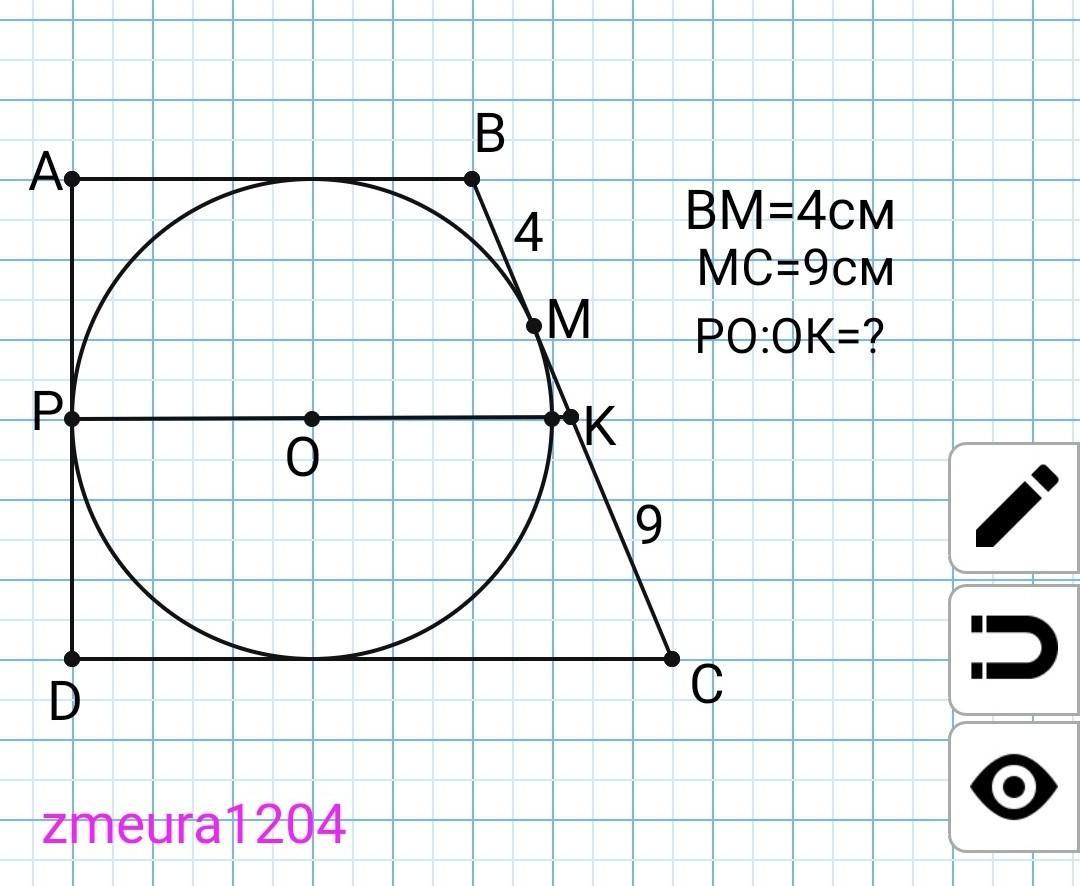
В прямоугольную трапецию АВСD вписана окружность. Боковая сторона ВС делится точкой соприкосновения окружности на отрезки 4 см и 9 см, считая от вершины В. Найдите отношение длин отрезков, на которые центр окружности делит среднюю линию трапеции.

Answer 1

Ответ:

РО:ОК=6:6,5

Объяснение:

r=√(BM*MC)=√(4*9)=6см

АD=h=2r=2*6=12см

В трапецию вписана окружность, то выполняется условие:

АD+BC=AB+DC

AD+BC=12+4+9=25см

РК=(АВ+DC)/2=25/2=12,5см

РО=r=6см

OK=PK-PO=12,5-6=6,5см

РО:ОК=6:6,5