Ответы
Ответ дал:
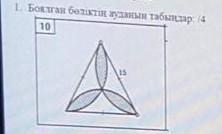
1
Ответ:
Sзакраш=75π-112,5√3 ед.кв
Объяснение:
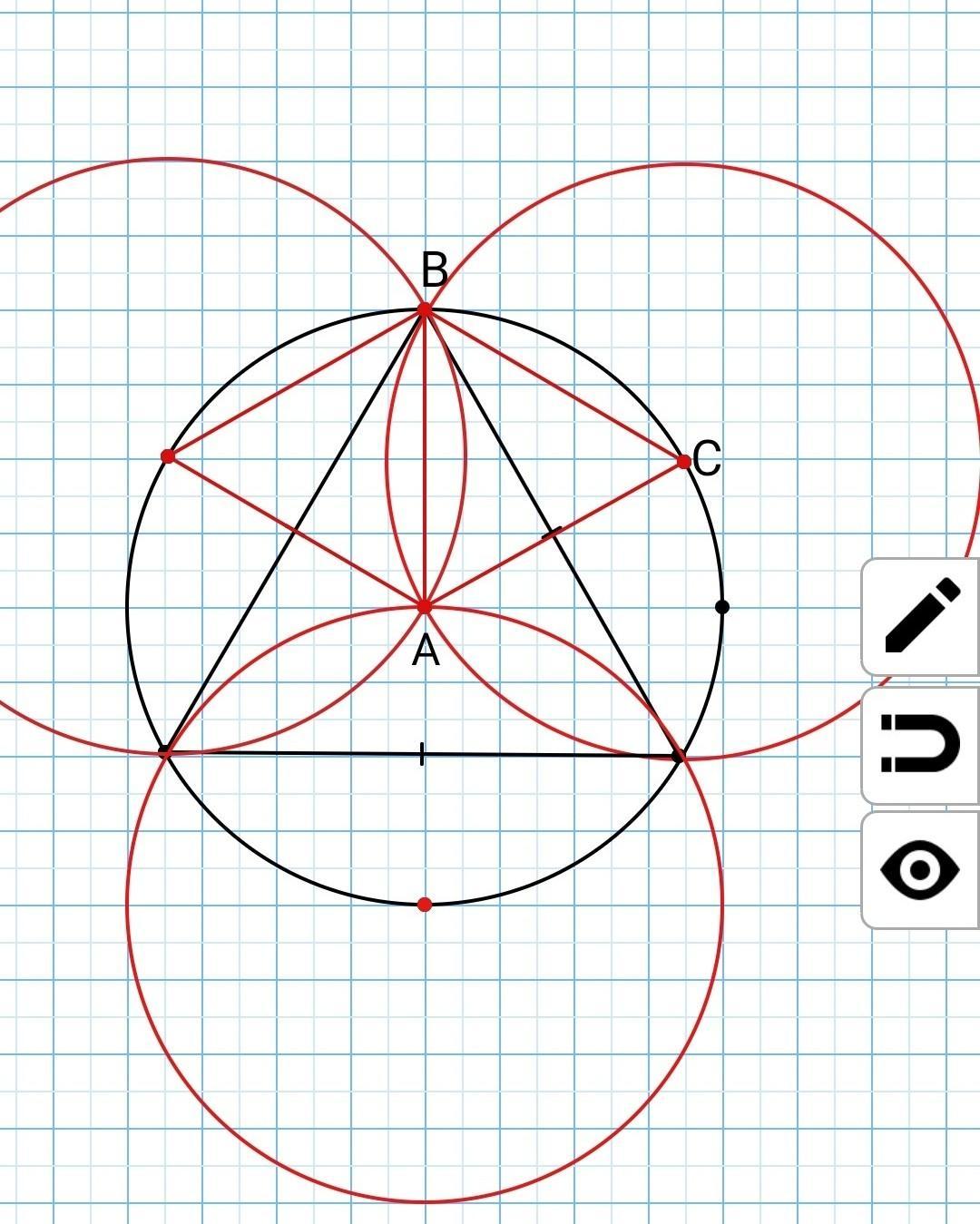
АВ=R- радиус описанной окружности равностороннего треугольника со стороной 15
R=a/√3=15/√3=5√3 ед.
∆АВС- равносторонний треугольник, со стороной 5√3 ед.
Найдем площадь сегмента АВ.
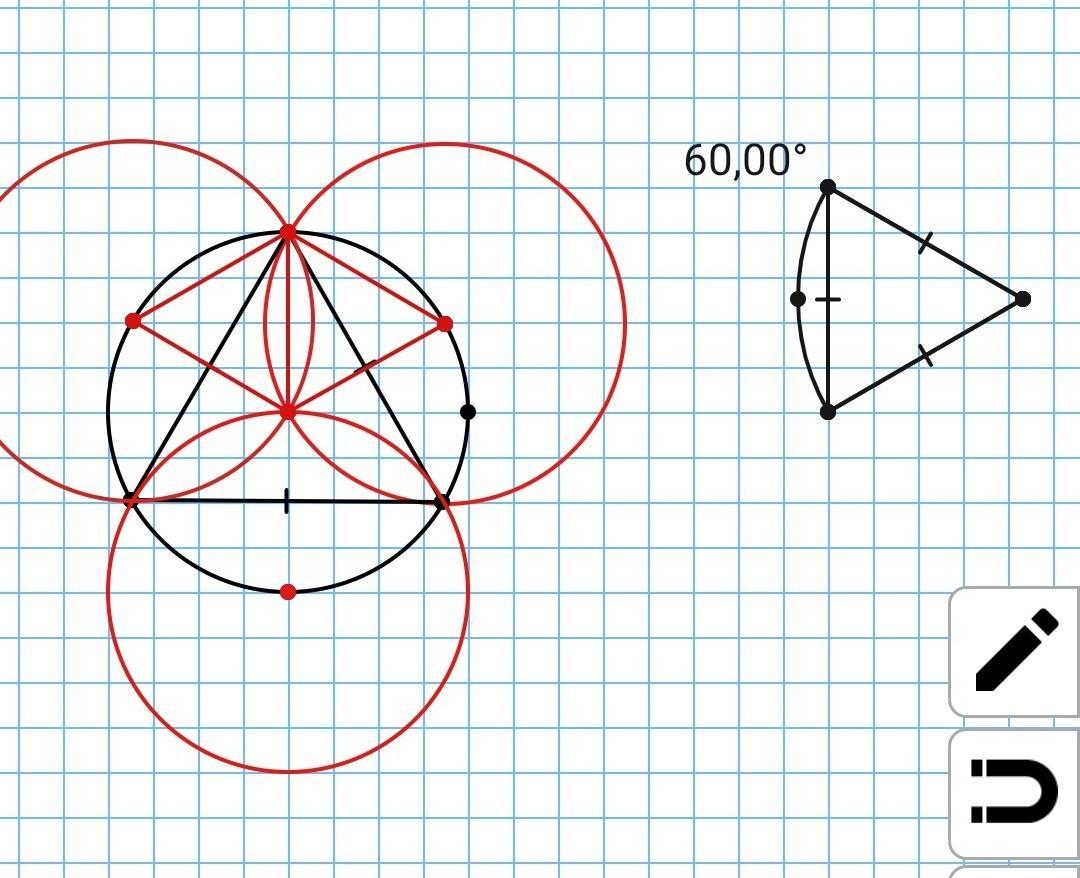
Для этого найдем площадь сектора (ВСА), с центральным углом ∠ВСА=60°, и отнимем площадь треугольника ∆АВС.
Sсект(ВСА)=π*ВС²*60°/360°=
=(5√3)²π/6=12,5π ед.кв.
S(∆ABC)=BC²√3/4=(5√3)²√3/4=
=75√3/4=18,75√3 ед.кв.
Sсегм=Sсект(ВСА)-S(∆ABC)=
=12,5π-18,75√3 ед.кв.
Таких сегментов 6 (цветок)
Sзакраш=6*Sсегм=
=6(12,5π-18,75√3)=75π-112,5√3 ед.кв.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад