Решите, только не с инета, потому что там не верное решение в трапеции основания равны 2 см и 6 см. а боковые стороны 8 см и 4√3 см. Найдите угол, который образует большая боковая сторона с большей основой трапеции.
Ответы
Ответ:
Угол, который образует большая боковая сторона с большей основой трапеции равен 60°.
Объяснение:
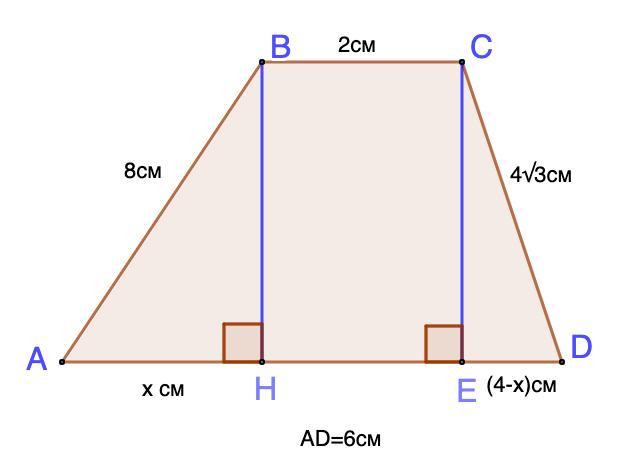
В трапеции основания равны 2 см и 6 см, а боковые стороны 8 см и 4√3 см. Найдите угол, который образует большая боковая сторона с большей основой трапеции.
Дано: ABCD - трапеция;
ВС = 2 см, AD = 8 см - основания;
АВ = 8 см; CD = 4√3 см.
Найти: угол, который образует большая боковая сторона с AD.
Решение:
Определимся с большей стороной. Сравним АВ и CD:
8 и 4√3
4 · 2 и 4√3
4√4 и 4√3
8 > 4√3
⇒ АВ - большая сторона ⇒ ∠А - искомый угол.
Проведем высоты ВН и СЕ.
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ ВН || CE
⇒ ЕВСЕ - параллелограмм.
- Противоположные стороны параллелограмма равны.
⇒ ВС = НЕ = 2 см, ВН = СЕ.
Пусть АН = х см, тогда ED = 6 - 2 - x = 4 - x (см)
Рассмотрим ΔАВН и ΔЕСD - прямоугольные.
Выразим ВН и СЕ.
Из Δ АВН:
по теореме Пифагора:
АВ² = АН² + ВН²
ВН² = 64 - х²
Из Δ ECD:
по теореме Пифагора:
CD² = ED² + CE²
CE² = 48 - (4 - х)² = 48 - 16 + 8x - x² = 32 + 8x - x²
Так как ВН = СЕ, то можем составить уравнение:
64 - х² = 32 + 8х - х²
8х = 32 |:8
x = 4
⇒ AH = 4 см
Рассмотрим ΔАВН - прямоугольный.
АВ = 8 см - гипотенуза; АН = 4 см - катет.
- Если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то он лежит против угла 30°.
⇒ ∠АВН = 30°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠А = 90° - ∠АВН = 90° - 30° = 60°
Угол, который образует большая боковая сторона с большей основой трапеции равен 60°.