Срочно ‼️‼️ Даю 30 баллов.
Надо решить с помощью теоремы Пифагора,без всяких cos,sin
Окружность с центром O и радиусом 12см описана около треугольника MNK так,что угол MON=120°, угол NOK=90°.Найдите стороны MN и NK треугольника.
Ответы
Решение .
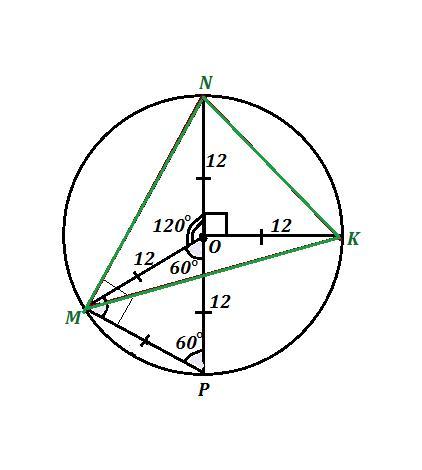
Дан ΔMNK . Около него описана окружность с центром в точке О и радиуса R=12 см . ∠MON = 120° , ∠NOK = 90° .
Найти стороны MN и NK .
Соединим центр О со всеми вершинами ΔMNK . И продлим радиус NO до пересечения с окружностью. Получим диаметр NP , NP = 2·12 = 24 см .
Рассмотрим ΔNOK . Он равнобедренный прямоугольный треугольник , так как его катетами являются радиусы описанной окружности , ON = OK = R = 12 см .
По теореме Пифагора можно найти гипотенузу NK этого треугольника : NK² = ON² + OK² = 12² + 12² = 288 ,
NK = √288 = 12√2 см .
Соединим вершину М с точкой Р . Получим ΔMNP .
Так как NР - диаметр , а ∠NMP опирается на этот диаметр , то ∠MNP = 90° , и ΔMNP - прямоугольный . По теореме Пифагора легко будет найти катет MN , если найти предварительно катет МР .
А МР найдём из треугольника ΔMON .
По условию ∠MON = 120° . Этот угол является смежным с углом ∠МОР , значит ∠MOP = 180° - ∠MON = 180°-120° = 60° .
ΔЬОР - равнобедренный , так как его сторонами являются радиусы описанной окружности : МО = ОР = 12 см .
Получили, что в равнобедренном треугольнике МОР угол МОР равен 60° , а значит это треугольник равносторонний и МР = 12 см .
Теперь применим теорему Пифагора в ΔMNP .
NP² = MP²+MN² ⇒ MN² = NP²- MP² = 24² - 12² = 432 ,
MN = √432 = 12√3 см .
P.S. Конечно, быстрее было бы найти сторону MN по теореме косинусов для равнобедренного ΔMON .
Ответ: MN = 12√3 см , NK = 12√2 см .