Ответы
Ответ дал:
2
Ответ:
Вычислить сумму ряда .
Представим общий член ряда в виде :
Такое разложение можно получить , применяя метод неопределённых коэффициентов.
Дроби равны, их знаменатели равны, приравниваем числители .
Многочлены равны при любых значениях n . Придаём n удобное значение и вычисляем неизвестный коэффициент.
Теперь составляем n-ую частичную сумму ряда и находим её предел . Чем больше членов суммы мы выпишем, тем понятнее будет, какие члены ряда в сумме дадут нули .
Сумма ряда равна 0,25 .
Помогите пожалуйста
a)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
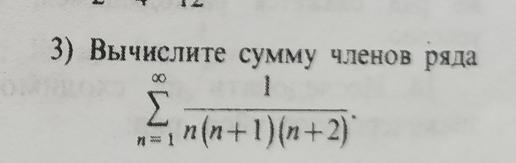
а) 1; 4; 16; 64....
б) 12; 9; 6; 3....
в) 1; 3; 6; 9....
г) -10; -8; -6....