6. Спростіть вираз x/(x - 5) - (x + 3)/(6x - 30) * 150/(3x + x ^ 2)
7. Розв'яжіть рівняння (x ^ 4 - x ^ 2 - 12)/(x + 2) = 0
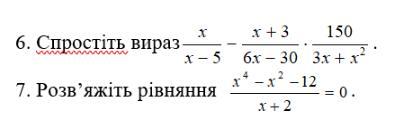
Ответы
Давайте спростимо вираз:
x/(x - 5) - (x + 3)/(6x - 30) * 150/(3x + x^2)
Спочатку спростимо перший доданок:
x/(x - 5) = x * 1/(x - 5) = x/(x - 5)
Далі спростимо другий доданок:
(x + 3)/(6x - 30) * 150/(3x + x^2) = (x + 3)/(6(x - 5)) * 150/(x(x + 3))
Зараз зводимо до спільного знаменника:
(x(x + 3))/(6(x - 5)) * 150/(x(x + 3)) = (150x(x + 3))/(6(x - 5)x(x + 3))
Зараз спрощуємо спільні множники (x + 3) та x:
(150x(x + 3))/(6(x - 5)x(x + 3)) = 150/(6(x - 5)x)
В результаті отримуємо спрощений вираз:
150/(6(x - 5)x)
Далі розв'яжемо рівняння:
(x^4 - x^2 - 12)/(x + 2) = 0
Спочатку факторизуємо чисельник:
(x^4 - x^2 - 12) = (x^2 - 4)(x^2 + 3)
Тепер ми можемо записати рівняння таким чином:
(x^2 - 4)(x^2 + 3)/(x + 2) = 0
Розкладаємо доданки на множники:
(x - 2)(x + 2)(x^2 + 3)/(x + 2) = 0
Скорочуємо спільні множники:
(x - 2)(x^2 + 3) = 0
Застосовуємо властивість добутку дорівнює нулю:
x - 2 = 0 або x^2 + 3 = 0
Розв'язуємо обидва рівняння:
x - 2 = 0 -> x = 2
x^2 + 3 = 0 -> x^2 = -3 (рівняння не має дійсних розв'язків)
Отже, рівняння має один дійсний розв'язок: x = 2.