Question

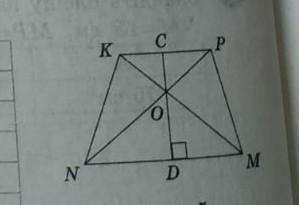
10 У трапеції NKPM основи дорівнюють 12 см і 18 см, а висота 15 см (рис. 5). Знайдіть площі трикутників NKO i POM.​

Answer 1

Для знаходження площі трикутника необхідно знати його висоту і одну зі сторін. У трапеції NKPM, трикутники NKO і POM мають однакову висоту, але різні основи.

Площа трикутника NKO може бути знайдена за формулою: S(NKO) = (1/2) * основа * висота.

Площа трикутника POM також може бути знайдена за формулою: S(POM) = (1/2) * основа * висота.

В даному випадку, висота трикутників NKO і POM однакова і дорівнює 15 см.

Площа трикутника NKO: S(NKO) = (1/2) * 12 см * 15 см = 90 см².

Площа трикутника POM: S(POM) = (1/2) * 18 см * 15 см = 135 см².